Chapters

Exercise 1
Exercise 2
Exercise 3
Exercise 4
Exercise 5
Exercise 6
Exercise 7
Exercise 8
Solution of exercise Solved Complex Number Word Problems
Solution of exercise 1
Solution of exercise 2
Solution of exercise 3
Solution of exercise 4
Solution of exercise 5
Solution of exercise 6
Solution of exercise 7
Solution of exercise 8

The best Maths tutors available

Exercise 1

Calculate the value of k for the complex number obtained by dividing . Note, it is represented in the bisector of the first quadrant.

Exercise 2

Find the value of k for the quotient , if it is:

1 A pure imaginary number.

2 A real number.

Exercise 3

The complex number, 2 + 2 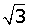is rotated 45° about the origin of its coordinates in an anti-clockwise direction. Find the complex number obtained after the turn.

Exercise 4

Find the coordinates of the vertices of a regular hexagon of center origin, knowing that one of its vertices is the affix of complex number, 1_90°_.

Exercise 5

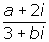
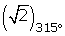
Determine the value of b for the quotient , if it equals:

Exercise 6

What are the coordinates of the point that is obtained on having turned the affix of the complex 2 + i, 90° in an counterclockwise direction about the origin.

Exercise 7

Find the coordinates of the vertices of a square of center origin, knowing that one vertex is the point (0, −2).

Exercise 8

The sum of the real components of two conjugate complex numbers is six, and the sum of its modulus is 10. Determine these complex numbers.

Solution of exercise Solved Complex Number Word Problems

Solution of exercise 1

Calculate the value of k for the complex number obtained by dividing 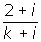. Note, it is represented in the bisector of the first quadrant.

For the affix, (a, b), the complex number is on the bisector of the first quadrant. The following must be met: a = b.

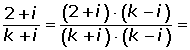
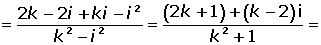
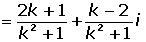
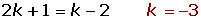
Solution of exercise 2

Find the value of k for the quotient 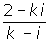, if it is:

1 A pure imaginary number.

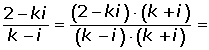
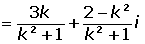
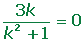
2 A real number.

Solution of exercise 3

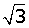
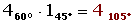
The complex number, 2 + 2 is rotated 45° about the origin of its coordinates in an anti-clockwise direction. Find the complex number obtained after the turn.

Solution of exercise 4

Find the coordinates of the vertices of a regular hexagon of center origin, knowing that one of its vertices is the affix of complex number, 1_90°_.

The vertices are the affixes of the sixth roots of another complex number, z.

z = (1_90°)⁶ = 1_540° = 1_180°

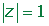
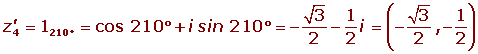
Solution of exercise 5

Determine the value of b for the quotient , if it equals:

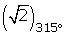
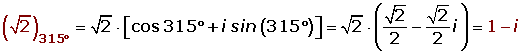
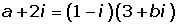
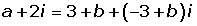
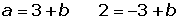
Solution of exercise 6

What are the coordinates of the point that is obtained on having turned the affix of the complex 2 + i, 90° in an counterclockwise direction about the origin.

(2 + i) · 1_90° = (2 + i) · i = −1 + 2i = (−1,2)

Solution of exercise 7

Find the coordinates of the vertices of a square of center origin, knowing that one vertex is the point (0, −2).

(0, −2) = −2 i = 2₂₇₀

The vertices are the affixes of the quarter roots of another complex number, z.

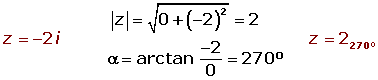
(2_270°)⁴ = 16_1080º = 16_{3 · 360°} = 16_0°

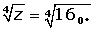
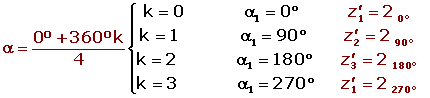
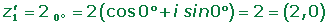
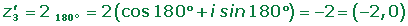
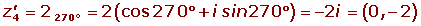
Solution of exercise 8

The sum of the real components of two conjugate complex numbers is six, and the sum of its modulus is 10. Determine these complex numbers.

z = a + bi = r_α

z = a − bi = r_−α

r + r = 10 r = 5

a + a = 6 a = 3

5² = 3² + b² b=4

r cos α + r cos (−α) = 6

5 cos α + 5 cos α = 6

cos α = 3/5

α = 53° 7' 48'' α = 306° 52' 11''

3 + 4i = 5_{53° 7' 48''}

3 − 4i = 5_{306° 52' 11''}

Did you like this article? Rate it!

4.00 (2 rating(s))

Emma

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Complex Number Word Problems

Exercise 1

Exercise 2

Exercise 3

Exercise 4

Exercise 5

Exercise 6

Exercise 7

Exercise 8

Solution of exercise Solved Complex Number Word Problems

Solution of exercise 1

Solution of exercise 2

Solution of exercise 3

Solution of exercise 4

Solution of exercise 5

Solution of exercise 6

Solution of exercise 7

Solution of exercise 8

Adding and Subtracting Complex Numbers

Complex Numbers

Equal, Conjugate, Opposite and Reciprocal Complex Numbers

Dividing Complex Numbers

Multiplying Complex Numbers

Complex Numbers in Polar Form

Power of a Complex Number

nth Root of a Complex Number

Imaginary Numbers

Complex Number Worksheets