Chapters

Introduction
 z=a+bi
z=a+bi
where a is any Real number and is known as the Real part of the Complex number, 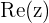 ,
,
and b is any Real number multiplied by  and is known as the Imaginary part of the Complex number,
and is known as the Imaginary part of the Complex number,  .
.
Example
If 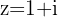 , then
, then 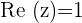 and
and  , which is multiplied by
, which is multiplied by 
The set of all Complex Numbers is denoted by 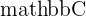 .
.
If  in the Complex number
in the Complex number 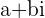 , then the number reduces to an ordinary Real number
, then the number reduces to an ordinary Real number 
Example
 3+0i=3
3+0i=3
A number of the form  is known as a pure Imaginary number
is known as a pure Imaginary number
Example
 4i
4i
 sqrt{-25}=sqrt{25i^{2}}=5i
sqrt{-25}=sqrt{25i^{2}}=5i
Equality of 2 Complex Numbers
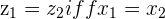 and
and 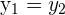
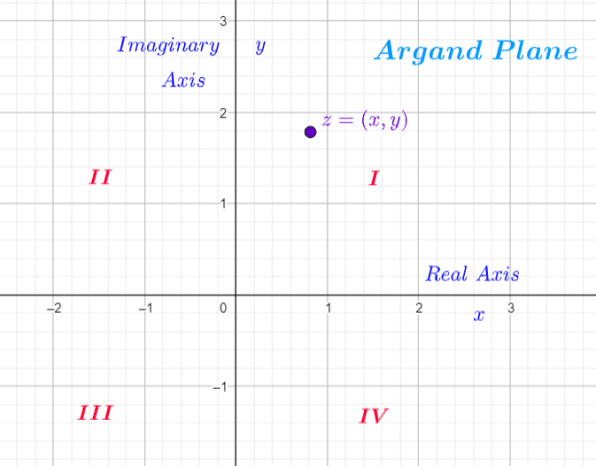
Complex Numbers in the Complex Plane
Complex numbers are multi-part because of the inclusion of both the Real and Imaginary parts in the whole Complex Number.
As for being 2-Dimensional, we equate the ordered pair  with a point
with a point 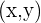 in the 2-Dimensional Complex or Argand plane
in the 2-Dimensional Complex or Argand plane
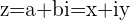 with
with  and
and 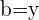
The Argand Plane
The Complex plane is a plane similar to the  -plane, with 2 axes and 4 quadrants. The
-plane, with 2 axes and 4 quadrants. The  is treated as an independent dimension and so is the
is treated as an independent dimension and so is the 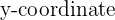 , which has all of its members multiplied by
, which has all of its members multiplied by  .
.
In the Complex plane, the  is the Real axis and the
is the Real axis and the 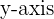 is the Imaginary axis.
is the Imaginary axis.
A Real number is represented by a number on the  and an Imaginary number is represented by a number on the
and an Imaginary number is represented by a number on the 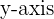 .
.
A Complex Number is 2-Dimensional and is represented by a point 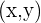 in the plane.
in the plane.
Example
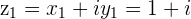 is the Complex number represented by the point
is the Complex number represented by the point 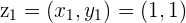 in the 1st Quadrant of the Argand plane
in the 1st Quadrant of the Argand plane
Example
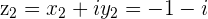 is the Complex number represented by the point
is the Complex number represented by the point 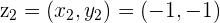 in the 3rd Quadrant of the plane
in the 3rd Quadrant of the plane

Complex Numbers as Vectors
Multidimensionality gives us the ability to graphically represent a Complex number with a vector quantity and an associated directed angle 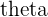 that the vector makes as measured counterclockwise from the positive
that the vector makes as measured counterclockwise from the positive  , with
, with 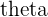 measured in radians and
measured in radians and
 0leqthetaleq2pi
0leqthetaleq2pi
The vector associated with each unique Complex number  is a vector emanating from the origin and directed to the point
is a vector emanating from the origin and directed to the point 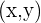 in the plane.
in the plane.
Example
 is not only the point
is not only the point  in the plane, it is also the vector emanating from the origin directed to the point
in the plane, it is also the vector emanating from the origin directed to the point  .
.
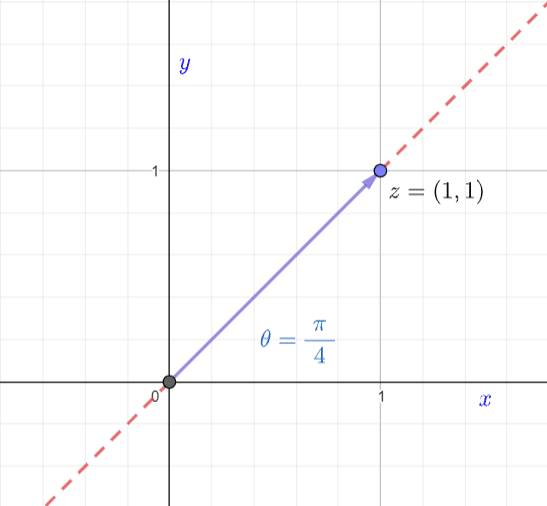
We can see geometrically that along this vector, 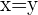 and the associated angle would be
and the associated angle would be 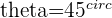 or
or 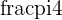 , because a line coincident with the vector cuts the plane into 2 parts at a
, because a line coincident with the vector cuts the plane into 2 parts at a 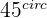 angle.
angle.
Argument of a Complex Number
The angle 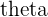 is called the argument of the Complex number
is called the argument of the Complex number  and is denoted by
and is denoted by 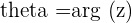 .
.
We can find the value of the argument by taking the inverse tangent or arctangent of the angle 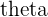 , which is the angle that has a tangent value of
, which is the angle that has a tangent value of 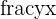
 theta=tan^{-1}(frac{y}{x})=arctan(frac{y}{x})
theta=tan^{-1}(frac{y}{x})=arctan(frac{y}{x})
Example
To check that the angle from the previous example is equivalent to 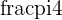 , we need to find the angle whose tangent is equal to
, we need to find the angle whose tangent is equal to  , because
, because  and
and  and their ratio
and their ratio 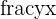 is also equal to
is also equal to 
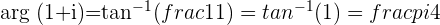
Range of the Argument
All angles will be measured in radians and we limit the range for the directed angle 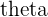 to
to  so as to have a unique angle measure for each vector associated with a unique point, because the angle can have an infinite number of equivalent values past
so as to have a unique angle measure for each vector associated with a unique point, because the angle can have an infinite number of equivalent values past  .
.
Reference Angles
The argument is always a reference angle between  and
and  and if the angle is larger than
and if the angle is larger than  we determine the reference angle by subtracting multiples of
we determine the reference angle by subtracting multiples of  from the original angle.
from the original angle.
Example
If 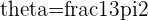 , we must subtract
, we must subtract  from it to find the argument
from it to find the argument

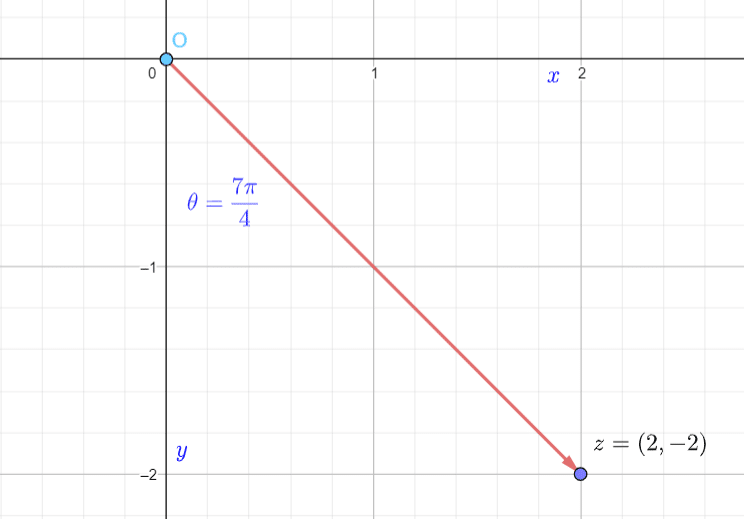
Example
If 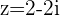 , we know the point is located in the 4th Quadrant because
, we know the point is located in the 4th Quadrant because 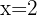 and
and  .
.
We must always be careful to keep track of minus signs and where exactly the point is located, so as not to confuse angles or quadrants.

Negative Arguments
An angle 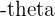 is an angle measured clockwise from the positive
is an angle measured clockwise from the positive  and it has an equivalent but opposite range from
and it has an equivalent but opposite range from  .
.
An angle measure that is negative, 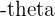 , is equivalent to an angle measure of
, is equivalent to an angle measure of 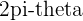 .
.
Modulus of a Complex Number
We can resolve any vector into its respective  and
and  components and use the Pythagorean Theorem to find its length.
components and use the Pythagorean Theorem to find its length.
The length of a vector is the distance from the origin to the tip and is known as its magnitude. The magnitude of the vector associated with each Complex number  is known as its modulus or absolute value and is found by taking the square root of the sum of the squares of its components
is known as its modulus or absolute value and is found by taking the square root of the sum of the squares of its components
 |z|=sqrt {x^{2}+y^{2}}
|z|=sqrt {x^{2}+y^{2}}
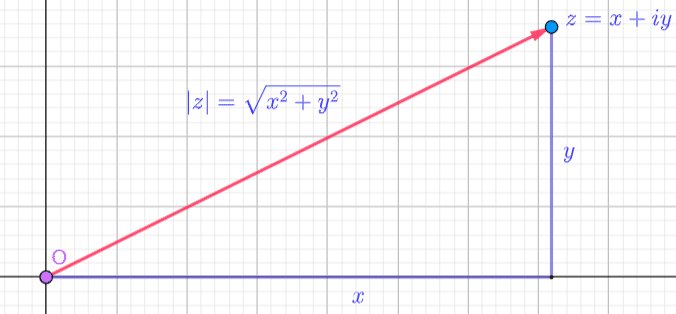
The modulus is always a non-negative Real number
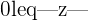 with
with 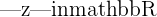 and
and  and
and 
Example
 and
and 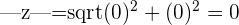
Example
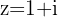 and
and 
Example
 and
and 
Magnitude of a Complex Number's Opposite
The magnitude of a Complex number and its negative or opposite are equal in value because the square of a number and the square of its negative are always equal
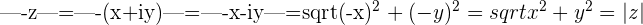













It is a good for me for giving some help in order to understand very well
this qwestion is necessary
l need support for complex numbers , inverse of quadratic equation, set theory