
¿Cómo podemos usar la programación lineal en la vida diaria?
La programación lineal se utiliza cuando buscamos la solución más óptima para un problema de la vida de cada día, considerando las restricciones. Para poder encontrar la solución, necesitamos formular un problema de la vida real usando un modelo matemático. En los próximos ejercicios de programación lineal, buscamos por una parte, la solución ideal para minimizar el coste de una empresa de transporte, y por la otra, para minimizar el coste de una excursión de escuela.
Problemas de programación lineal
1 Una empresa de transportes tiene dos tipos de camiones, los del tipo A con un espacio refrigerado de  y un espacio no refrigerado de
y un espacio no refrigerado de  . Los del tipo B, con igual cubicaje total, al
. Los del tipo B, con igual cubicaje total, al  de refrigerado y no refrigerado. La contratan para el transporte de
de refrigerado y no refrigerado. La contratan para el transporte de  de producto que necesita refrigeración y
de producto que necesita refrigeración y  de otro que no la necesita. El coste por kilómetro de un camión del tipo A es de
de otro que no la necesita. El coste por kilómetro de un camión del tipo A es de  € y el B de
€ y el B de  €. ¿Cuántos camiones de cada tipo ha de utilizar para que el coste total sea mínimo?
€. ¿Cuántos camiones de cada tipo ha de utilizar para que el coste total sea mínimo?
 camiones de tipo A
camiones de tipo A
 camiones de tipo B
camiones de tipo B
2 Función objetivo

3 Restricciones
| A | B | Total | |
|---|---|---|---|
| Refrigerado | 20 | 30 | 3 000 |
| No refrigerado | 40 | 30 | 4 000 |




4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo


Como  e
e  han de ser números naturales redondeamos el valor de
han de ser números naturales redondeamos el valor de  .
.

Por defecto, veamos que valor toma la  para
para  en la ecuación
en la ecuación  que pertenece al recinto de las soluciones factibles;
que pertenece al recinto de las soluciones factibles;  . Obtenemos un número natural
. Obtenemos un número natural

El coste mínimo son  € para
€ para  y
y  .
.
¿Buscas un profesor de matematicas a domicilio? ¡Encuéntralo en Superprof!
2 Una escuela prepara una excursión para  alumnos. La empresa de transporte tiene
alumnos. La empresa de transporte tiene  autobuses de
autobuses de  plazas y
plazas y  de
de  plazas, pero sólo dispone de
plazas, pero sólo dispone de  conductores. El alquiler de un autocar grande cuesta
conductores. El alquiler de un autocar grande cuesta  € y el de uno pequeño
€ y el de uno pequeño  €. Calcular cuántos autobuses de cada tipo hay que utilizar para que la excursión resulte lo más económica posible para la escuela.
€. Calcular cuántos autobuses de cada tipo hay que utilizar para que la excursión resulte lo más económica posible para la escuela.
 autobuses pequeños
autobuses pequeños
 autobuses grandes
autobuses grandes
2 Función objetivo

3 Restricciones





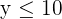
4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
 €
€
 € Mínimo
€ Mínimo
El coste mínimo es de  €, y se consigue
€, y se consigue  autobuses grandes y
autobuses grandes y  pequeños.
pequeños.
3 Una fábrica de textiles produce dos tipos de prendas A y B con concentraciones distintas de poliéster y algodón. La prenda del modelo A requiere  onzas de poliéster y
onzas de poliéster y  de algodón, mientras la prenda del modelo B necesita
de algodón, mientras la prenda del modelo B necesita  onzas de poliéster y
onzas de poliéster y  de algodón. La empresa cuenta con
de algodón. La empresa cuenta con  onzas de poliéster y
onzas de poliéster y  de algodón. La utilidad marginal de la prenda A es de
de algodón. La utilidad marginal de la prenda A es de  € y de cada prenda B es de
€ y de cada prenda B es de  €. Determina la cantidad óptima de unidades de prendas A y B que deben fabricarse para maximizar la utilidad por la venta de las prendas.
€. Determina la cantidad óptima de unidades de prendas A y B que deben fabricarse para maximizar la utilidad por la venta de las prendas.
 número de prendas del modelo A
número de prendas del modelo A
 número de prendas del modelo B
número de prendas del modelo B
2 Función objetivo

3 Restricciones




4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
 €
€
 €
€
 €
€
La utilidad máxima posible es de  €, y ocurre cuando los niveles de producción son de
€, y ocurre cuando los niveles de producción son de  y
y  prendas de los modelos A y B, respectivamente.
prendas de los modelos A y B, respectivamente.
¿Prefieres aprender desde casa? Entra en Superprof, ¡y encuentra ya a tu profesor online de matematicas!
4 En la misma fábrica del ejercicio 3 cambiamos las utilidades. En una fábrica se producen produce dos tipos de prendas A y B con concentraciones distintas de poliéster y algodón. La prenda del modelo A requiere  onzas de poliéster y
onzas de poliéster y  de algodón, mientras la prenda del modelo B necesita
de algodón, mientras la prenda del modelo B necesita  onzas de poliéster y
onzas de poliéster y  de algodón. La empresa cuenta con
de algodón. La empresa cuenta con  onzas de poliéster y
onzas de poliéster y  de algodón. La utilidad marginal de la prenda A es de
de algodón. La utilidad marginal de la prenda A es de  € y de cada prenda B es de
€ y de cada prenda B es de  €. Determina la cantidad óptima de unidades de prendas A y B que deben fabricarse para maximizar la utilidad por la venta de las prendas.
€. Determina la cantidad óptima de unidades de prendas A y B que deben fabricarse para maximizar la utilidad por la venta de las prendas.
 número de prendas del modelo A
número de prendas del modelo A
 número de prendas del modelo B
número de prendas del modelo B
2 Función objetivo

3 Restricciones




4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
 €
€
 €
€
 €
€
Los valores óptimos son todos los puntos del segmento de recta  que se encuentra sombreado; así el problema tiene soluciones óptimas alternativas que producen una utilidad máxima de
que se encuentra sombreado; así el problema tiene soluciones óptimas alternativas que producen una utilidad máxima de  €.
€.
5 En una granja se considera servir a los animales dos alimentos cada uno con contenido nutricional distinto. El primer alimento contiene  de aminoácido tipo 1 y
de aminoácido tipo 1 y  de aminoácido tipo 2, mientras que el segundo alimento contiene
de aminoácido tipo 2, mientras que el segundo alimento contiene  de aminoácido tipo 1 y
de aminoácido tipo 1 y  de aminoácido tipo 2. El costo por gramo del alimento 1 es de
de aminoácido tipo 2. El costo por gramo del alimento 1 es de  € y el costo por gramo del alimento tipo 2 es de
€ y el costo por gramo del alimento tipo 2 es de  €. Se puede servir cualquier combinación de los alimentos siempre y cuando se sirva al menos tres onzas del alimento tipo 2. Si la cantidad mínima diaria de aminoácido tipo 1 es de
€. Se puede servir cualquier combinación de los alimentos siempre y cuando se sirva al menos tres onzas del alimento tipo 2. Si la cantidad mínima diaria de aminoácido tipo 1 es de  y de
y de  , calcule el número de onzas que deben servirse a cada animal, de manera que el costo del alimento sea el más económico.
, calcule el número de onzas que deben servirse a cada animal, de manera que el costo del alimento sea el más económico.
1 Elección de las incógnitas.
 número de gramos del alimento 1
número de gramos del alimento 1
 número de gramo del alimento 2
número de gramo del alimento 2
2 Función objetivo

3 Restricciones




4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
 €
€
El valor óptimo es  . Por tanto, el costo mínimo de la comida de cada animal es de
. Por tanto, el costo mínimo de la comida de cada animal es de  €, lo cual sucede cuando se sirven
€, lo cual sucede cuando se sirven  onzas de alimento tipo 1 y
onzas de alimento tipo 1 y  onzas del tipo 2.
onzas del tipo 2.
6 Un comerciante acude a comprar peras y manzanas con  €. El productor le ofrece las peras a
€. El productor le ofrece las peras a  € el kilogramo y la manzana a
€ el kilogramo y la manzana a  € el kilogramo. Se sabe que en su vehículo solo puede transportar
€ el kilogramo. Se sabe que en su vehículo solo puede transportar  como máximo y piensa vender el kilogramo de pera a
como máximo y piensa vender el kilogramo de pera a  € y de manzana a
€ y de manzana a  €. El comerciante debe poner a disposición de sus clientes al menos
€. El comerciante debe poner a disposición de sus clientes al menos  de peras. Encuentra la cantidad en kilogramos de frutas que debe adquirir el comerciante para su venta de manera que maximice su utilidad.
de peras. Encuentra la cantidad en kilogramos de frutas que debe adquirir el comerciante para su venta de manera que maximice su utilidad.
1 Elección de las incógnitas.
 número de kilogramos de pera
número de kilogramos de pera
 número de kilogramos de manzana
número de kilogramos de manzana
2 Función objetivo

3 Restricciones




4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
 €
€
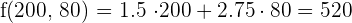 €
€
El valor óptimo es  y produce una utilidad máxima de
y produce una utilidad máxima de  €.
€.
7 Una empresa dedicada a la producción de artículo decorativos cuenta con  unidades de material y
unidades de material y  horas de mano de obra. Para producir el primer tipo de artículo decorativo se requiere
horas de mano de obra. Para producir el primer tipo de artículo decorativo se requiere  unidades de material y
unidades de material y  horas de trabajo; para producir el segundo tipo de artículo se requieren
horas de trabajo; para producir el segundo tipo de artículo se requieren  unidades de material y
unidades de material y  horas de mano de obra. La ganancia que obtiene por el primer artículo es de
horas de mano de obra. La ganancia que obtiene por el primer artículo es de  € y de
€ y de  € por el segundo. Encuentra la cantidad de artículos de ambos tipos que deben fabricarse para maximizar las ganancias si la empresa prometió construir al menos un artículo del primer tipo.
€ por el segundo. Encuentra la cantidad de artículos de ambos tipos que deben fabricarse para maximizar las ganancias si la empresa prometió construir al menos un artículo del primer tipo.
1 Elección de las incógnitas.
 número de artículos decorativos de tipo 1
número de artículos decorativos de tipo 1
 número de artículos decorativos de tipo 2
número de artículos decorativos de tipo 2
2 Función objetivo

3 Restricciones




4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
 €
€
 €
€
El valor óptimo es  y produce una máxima de
y produce una máxima de  €.
€.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Desde un puerto maritimo se an transportado 2 modelos de refrigeradosas. par barca asia una ciudad donde seran vendidos. para el transporte sea determinado que entre ambos modelos sean por lo menos 60 unidades pero 80 unidades. bs del modelo 1 no deben ser menes de 40 ni ma’s de se dispone de doo pies cuadrados os material para embalaje. cara refrigeradora del modelo & requiere 6 pias cusabrados del material para embalaje y la del modela 2 spies cuadrados de dicho material. el costo de transporte de una refrijedadora del modelo 1 esde 25 dolares yuno del modelo 2 de 15 dalares plantee un modela de programanión lineal y determine la solucción optima por el metodo geométrico
Una empresa que produce dos productos diferentes en dos plantas desea saber las cantidades optimas que permiten maximizar su beneficio, sabiendo que el primer producto puede ser vendido a 20 unidades monetarias, el segundo a 40 y que la planta A gasta dos horas hombre de trabajo en la producción del bien 1; dos horas de trabajo para producir el bien 2 y que cuenta con un máximo de 60. En la planta B tarda una hora hombre en producir el bien 1 y dos horas en producir el bien 2 y cuenta con un máximo de 40 horas en resolver el problema de la empresa utilizando el método gráfico.
la empresa de textil produce 200 m de tela de alpaca 6000 bolivianos y 150 m a razón d 37500bs cuánto cuesta producir 400 m de tela de alpaca
resuélvame este por favor:El “Expreso de Oriente” que realiza viajes entre Paris y Estambul, ofrece boletos para “Servicio Royalty” a un precio de $2.000 y “servicio General” a un precio de $1.000. El expreso tiene 200 asientos y requiere un límite de equipaje de hasta 800 kg. Al pasajero de “Servicio General” se le permite transportar un máximo de 20 Kg y al pasajero de “Servicio Royalty”, 50 Kg. de peso. Por política de la empresa, se debe ofertar a lo más el triple de asientos de “Servicio General” que los de “Servicio Royalty”. Si la empresa desea alcanzar un máximo de ingreso por ventas. Plantee y describa las variables de decisión, exprese la función objetivo y plantee las restricciones del problema.
LA EMPRESA “ABC” atiende los turistas que llegan diariamente. Esta dispone de los siguientes jugos: 150 litros de limón, 250 litros de parchita, 200 Litros de Naranja y 120 litros de Piña, la misma debe preparar dos mezclas con los jugos que vende que son: Jugo Coctel y Jugo de frutas. Considerando que la demandas siempre excede la existencia de la empresa y el resto de cada mezcla lo constituye un contenido muy barato.
El jugo Coctel debe contener por lo menos 15% de Jugo de limón 40% juga de piña y el jugo de frutas debe contener al menos 25% jugo de naranja, 30% de parchita y 20% de piña. Que rango de proporción se debe usar de cada jugo en las mezclas!? Defina las Variables de decisión respectivas
Una planta produce 2 tipos de computadores, A y B. Hay 2 líneas de producción, una dedicada a la producción de computadores de tipo A y la otra dedicada a la producción de computadores de tipo B. La capacidad de producción de la Línea A es de 60 unidades por día, la capacidad de la línea B es de 50 unidades por día. A requiere 20 minutos de Mano de Obra, mientras que B requiere 40 minutos de Mano de obra. Actualmente, hay un máximo de 40 horas de Mano de obra por día que puede ser asignado a cada una de las líneas. ¿La contribución a las ganancias es de $20 por computador de tipo A, y $30 del tipo B. Cual debería ser la estrategia de producción óptima por día?
una. contadora elaborar formato de devolución de impuestos a personas físicas y pequeña empresa. en promedio de cada devolución a personas requiere de la contado y una hora de tiempo de computadora. cada devolución s empresa requiere cuatro horas de tiempo de la contadora 2 horas de la computadora debeido a otra consideración de la empresa el tiempo edta limitado a 240 horas y el tiempo de la computadora esta limitada a 100horas
6. Se van a fabricar dos tipos de juguetes, el primero requiere de 80 gramos de plástico y 5 gramos de pintura. El segundo necesita 60 gramos de plástico y 9 gramos de pintura. Esta semana contara 48 kg de plástico y 4.5 kg de pintura. ¿Cuántos juguetes de cada tipo se deben fabricar si la utilidad unitaria que dejan al negocio es de $6?00 y $7.00 respectivamente? y graficar