Temas
- Optimizan en la fabricación de lamparas
- Material escolar
- Optimización para la alimentación en granja
- Programación lineal en la elaboración de medicinas
- Ejercicio sobre ofertas de ropa
- Producción de calculadoras
- Promociones en ventas de sillas y mesas
- Ventas de ollas
- Siembra de maíz y cebada
- Transporte de trabajadores
En este artículo resolveremos paso a paso ejercicios sobre programación lineal. Recordemos que, la programación lineal da respuesta a situaciones en las que se exige maximizar o minimizar funciones que se encuentran sujetas a determinadas limitaciones, que llamamos restricciones. Aplicaremos esta herramienda de las matemáticas para resolver problemas de optimización en áreas como en la industria, economía, etc.

Optimizan en la fabricación de lamparas
1Una compañía fabrica y venden dos modelos de lámpara L1 y L2. Para su fabricación se necesita un trabajo manual de 20 minutos para el modelo L1 y de 30 minutos para el L2; y un trabajo de máquina de 20 minutos para el modelo L1 y de 10 minutos para L2.
Se dispone para el trabajo manual de 100 horas al mes y para la máquina 80 horas al mes. Sabiendo que el beneficio por unidad es de 15 y 10 euros para L1 y L2, respectivamente, planificar la producción para obtener el máximo beneficio.
1 Elección de las incógnitas.
 = nº de lámparas L1
= nº de lámparas L1
 = nº de lámparas L2
= nº de lámparas L2
2 Función objetivo

3 Restricciones
Pasamos los tiempos a horas
20 min = 1/3 h
30 min = 1/2 h
10 min = 1/6 h
Para escribir las restricciones vamos a ayudarnos de una tabla:
| L1 | L2 | Tiempo | |
|---|---|---|---|
| Manual | 1/3 | 1/2 | 100 |
| Máquina | 1/3 | 1/6 | 80 |
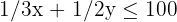

Como el número de lámparas son números naturales, tendremos dos restricciones más:
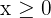

4 Hallar el conjunto de soluciones factibles
Tenemos que representar gráficamente las restricciones.
Al ser 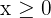 e
e  , trabajaremos en el primer cuadrante.
, trabajaremos en el primer cuadrante.
Representamos las rectas, a partir de sus puntos de corte con los ejes.
Resolvemos gráficamente la inecuación: 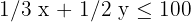 ; para ello, tomamos un punto del plano, por ejemplo el
; para ello, tomamos un punto del plano, por ejemplo el  .
.


La zona de intersección de las soluciones de las inecuaciones sería la solución al sistema de inecuaciones, que constituye el conjunto de las soluciones factibles.

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
La solución óptima si es única se encuentra en un vértice del recinto. Estos son las soluciones a los sistemas:
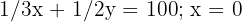
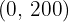
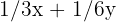
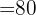 ;
; 
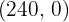
 ;
; 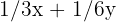
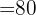


6 Calcular el valor de la función objetivo
En la función objetivo sustituimos cada uno de los vértices.
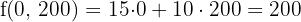 €
€
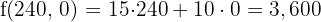 €
€
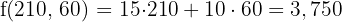 € Máximo
€ Máximo
La solución óptima es fabricar 210 del modelo L1 y 60 del modelo L2 para obtener un beneficio de 3,750€.
Material escolar
2Con el comienzo del curso se va a lanzar unas ofertas de material escolar. Unos almacenes quieren ofrecer 600 cuadernos, 500 carpetas y 400 bolígrafos para la oferta, empaquetándolo de dos formas distintas; en el primer bloque pondrá 2 cuadernos, 1 carpeta y 2 bolígrafos; en el segundo, pondrán 3 cuadernos, 1 carpeta y 1 bolígrafo. Los precios de cada paquete serán 6.5 y 7 €, respectivamente. ¿Cuántos paquetes le conviene poner de cada tipo para obtener el máximo beneficio?
1 Elección de las incógnitas.


2 Función objetivo
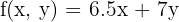
3 Restricciones
| P1 | P2 | Disponibles | |
|---|---|---|---|
| Cuadernos | 2 | 3 | 600 |
| Carpetas | 1 | 1 | 500 |
| Bolígrafos | 2 | 1 | 400 |

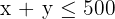

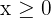
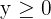
4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
 €
€
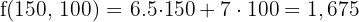 € Máximo
€ Máximo
La solución óptima son 150 P1 y 100 P2 con la que se obtienen 1,675€.
Si estás buscando clases particulares matematicas Zaragoza, ¡encuéntralas en Superprof!
Optimización para la alimentación en granja
3En una granja de pollos se da una dieta, para engordar, con una composición mínima de 15 unidades de una sustancia A y otras 15 de una sustancia B. En el mercado sólo se encuentra dos clases de compuestos: el tipo X con una composición de una unidad de A y 5 de B, y el otro tipo, Y, con una composición de cinco unidades de A y una de B. El precio del tipo X es de 10 euros y del tipo Y es de 30 €. ¿Qué cantidades se han de comprar de cada tipo para cubrir las necesidades con un coste mínimo?
1 Elección de las incógnitas.

2 Función objetivo
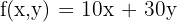
3 Restricciones
 |  | Mínimo | |
|---|---|---|---|
| A | 1 | 5 | 15 |
| B | 5 | 1 | 15 |
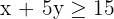

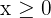

4 Hallar el conjunto de soluciones factibles
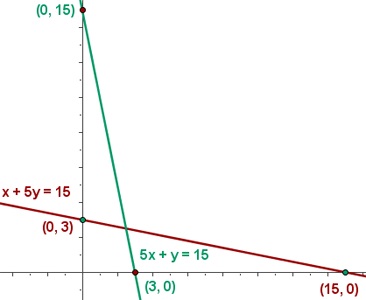
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
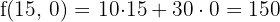 €
€
 € Mínimo
€ Mínimo
El coste mínimo son 100€ para X=5/2 e Y=5/2.
Programación lineal en la elaboración de medicinas
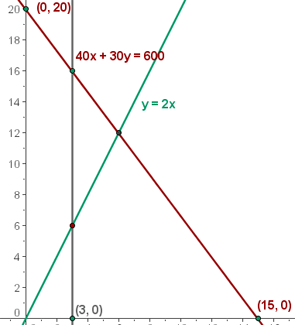
4Se dispone de 600 g de un determinado fármaco para elaborar pastillas grandes y pequeñas. Las grandes pesan 40 g y las pequeñas 30 g. Se necesitan al menos tres pastillas grandes, y al menos el doble de pequeñas que de las grandes. Cada pastilla grande proporciona un beneficio de 2 € y la pequeña de 1 €. ¿Cuántas pastillas se han de elaborar de cada clase para que el beneficio sea máximo?
1 Elección de las incógnitas.
 Número de pastillas grandes
Número de pastillas grandes
 Número de pastillas pequeñas
Número de pastillas pequeñas
2 Función objetivo

3 Restricciones

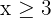

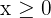

4 Hallar el conjunto de soluciones factibles
Repasa estos conceptos con clases particulares matematicas Madrid.
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

6 Calcular el valor de la función objetivo
 €
€
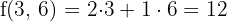 €
€
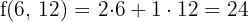 € Máximo
€ Máximo
El máximo beneficio es de 24€, y se obtiene fabricando 6 pastillas grandes y 12 pequeñas.
Ejercicio sobre ofertas de ropa
5Unos grandes almacenes desean liquidar 200 camisas y 100 pantalones de la temporada anterior. Para ello lanzan, dos ofertas, A y B. La oferta A consiste en un lote de una camisa y un pantalón, que se venden a 30 €; la oferta B consiste en un lote de tres camisas y un pantalón, que se vende a 50 €. No se desea ofrecer menos de 20 lotes de la oferta A ni menos de 10 de la B. ¿Cuántos lotes ha de vender de cada tipo para maximizar la ganancia?
1 Elección de las incógnitas.
 nº de lotes de A
nº de lotes de A
 nº de lotes de B
nº de lotes de B
2 Función objetivo

3 Restricciones
| A | B | Mínimo | |
|---|---|---|---|
| Camisas | 1 | 3 | 200 |
| Pantalones | 1 | 1 | 100 |

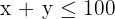


4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
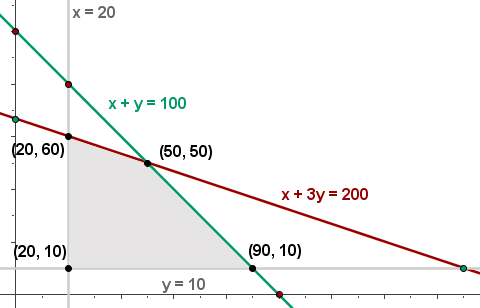
6 Calcular el valor de la función objetivo
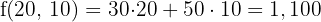 €
€
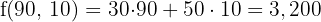 €
€
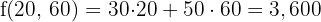 €
€
 € Máximo
€ Máximo
Con 50 lotes de cada tipo se obtiene una ganancia máxima de 4,000€.
Producción de calculadoras
6Una compañía produce dos tipos de calculadora, el modelo C1 y el modelo C2. El tiempo de fabricación de las calculadoras es de 1 hora para el modelo C1 y de 4 horas para el modelo C2. El costo de fabricación del modelo C1 es de 30€ y el costo del modelo C2 es de 20€. La compañía dispone de 1600 horas para fabricar las calculadoras y de 18000€ para gastos viables. La ganancia en cada calculadora del modelo C1 es de 10€ y la ganancia para el modelo C2 es de 8€. ¿Cuál debe ser el plan de producción para garantizar la máxima ganancia?
1 Elección de las incógnitas.
 nº de calculadoras C1
nº de calculadoras C1
 nº de calculadoras C2
nº de calculadoras C2
2 Función objetivo

3 Restricciones
| C1 | C2 | Disponible | |
|---|---|---|---|
| Horas | 1 | 4 | 1600 |
| Gastos | 30 | 40 | 18000 |
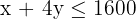

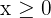

4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
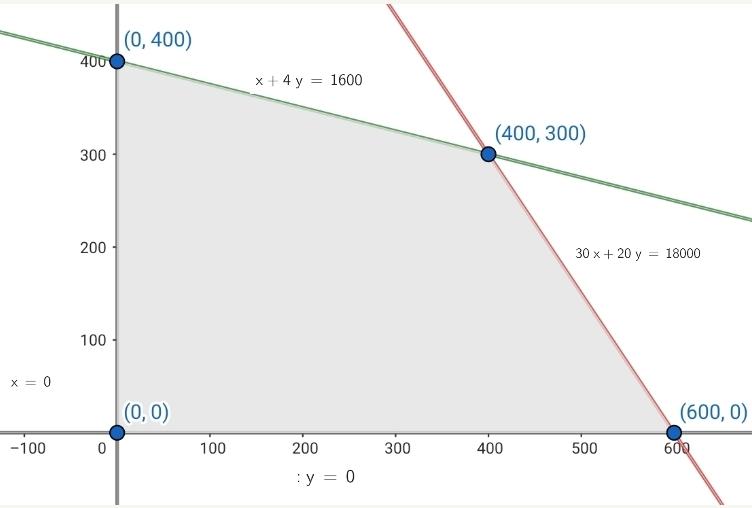
Los vértices son: 
6 Calcular el valor de la función objetivo
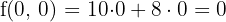 €
€
 €
€
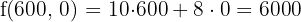 €
€
 € Máximo
€ Máximo
Con 400 calculadoras del modelo C1 y con 300 calculadoras del modelo C2 se obtiene la máxima ganancia de 7200€.
Promociones en ventas de sillas y mesas
7Un empresario desea vender 400 mesas y 200 sillas. Se ofrecen dos promociones, 1 y 2. La promoción 1 consiste en 1 mesa y en 1 silla, que se venden a 60€; la promoción 2 consiste en 3 mesas y en 1 silla, que se venden a 100€. No se desea ofrecer menos de 40 promociones de la oferta 1 ni menos de 20 promociones de la oferta 2. ¿Cuántas unidades debe producir la empresa para maximizar las ventas?
1 Elección de las incógnitas.
 nº de promociones 1 (P1)
nº de promociones 1 (P1)
 nº de promociones 2 (P2)
nº de promociones 2 (P2)
2 Función objetivo
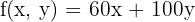
3 Restricciones
| P1 | P2 | Disponibles | |
|---|---|---|---|
| Mesas | 1 | 3 | 400 |
| Sillas | 1 | 1 | 200 |
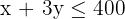
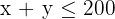


4 Hallar el conjunto de soluciones factibles
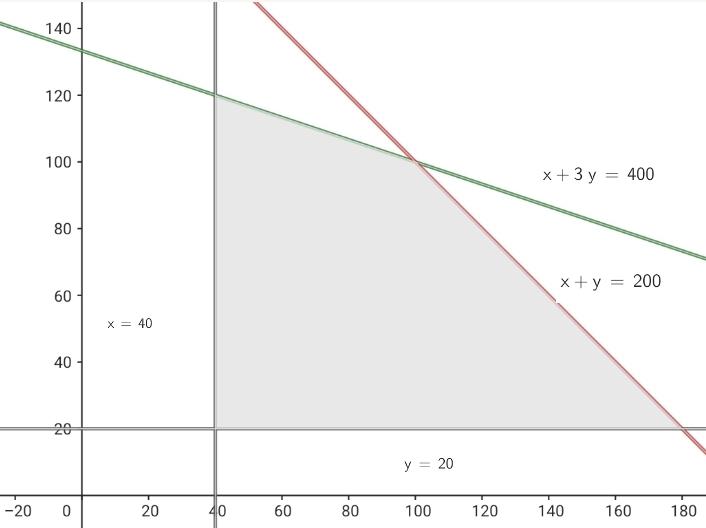
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
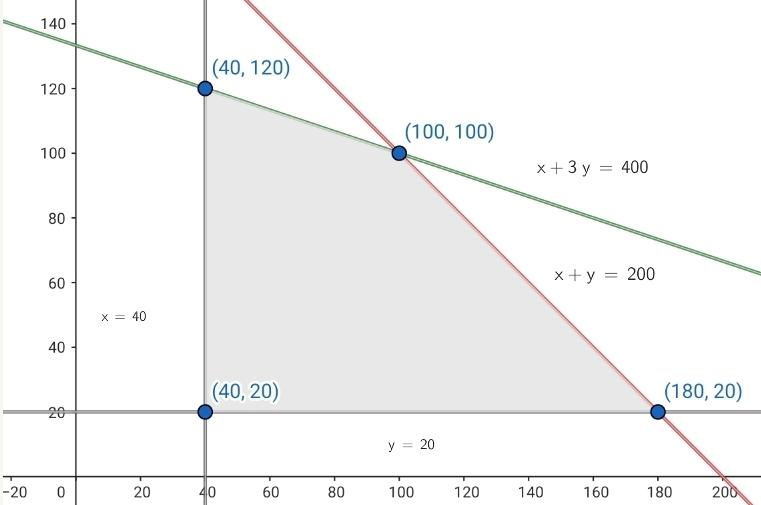
Los vértices son: 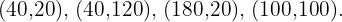
6 Calcular el valor de la función objetivo
 €
€
 €
€
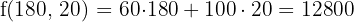 €
€
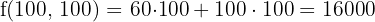 € Máximo
€ Máximo
Con 100 promociones de cada una se obtiene la ganancia máxima de 16000€.
Ventas de ollas
8Julián tiene un micro emprendimiento de ollas y pone a la venta una batería de cocina en dos presentaciones, una económica y otra de lujo. El gasto que tendrá de material es de 20€ para la económica y de 80€ para la de lujo. EL gasto de mano de obra es de 50€ para la económica y para la de lujo es de 80€. Julián dispone de 160,000€ para materiales y de 240,000€ para el pago de personal. Si la batería económica se vende en 100€ y la de lujo en 230€, ¿qué modelo de producción debe seguir Julián para que su venta sea máxima?
1 Elección de las incógnitas.
 nº de baterías económicas
nº de baterías económicas
 nº de baterías de lujo
nº de baterías de lujo
2 Función objetivo

3 Restricciones
| Económica | Lujo | Disponible | |
|---|---|---|---|
| Material | 20 | 80 | 160,000 |
| Mano de obra | 50 | 80 | 240,000 |
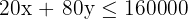
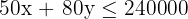


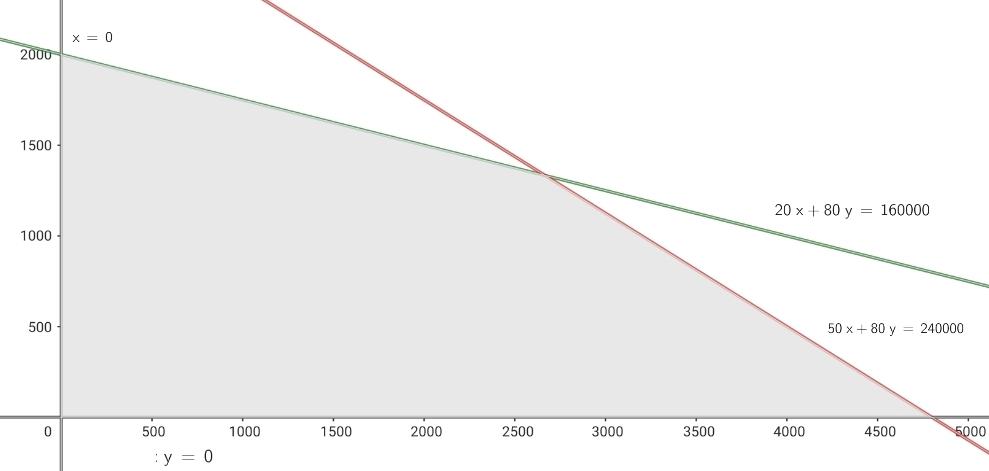
4 Hallar el conjunto de soluciones factibles
5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
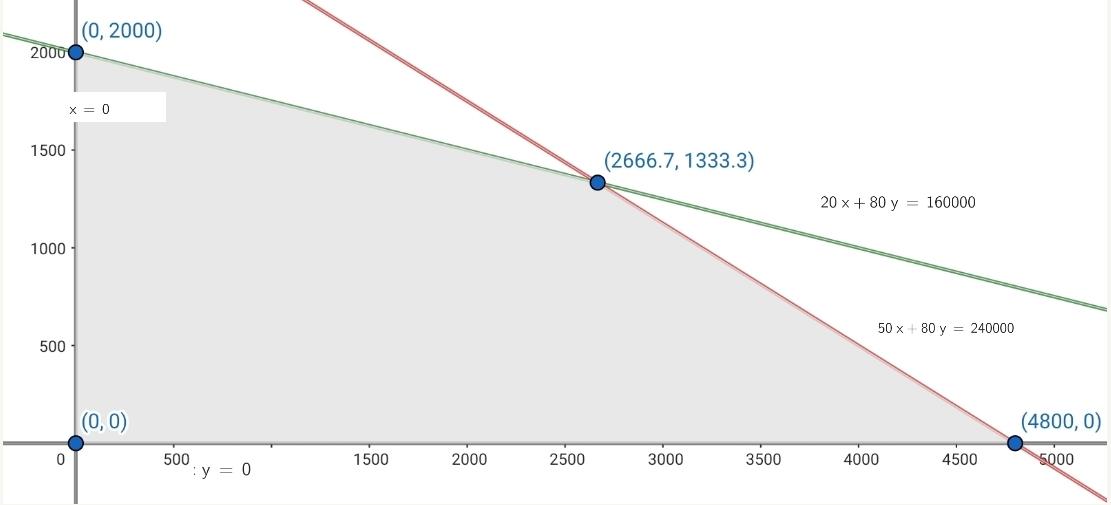
Los vértices son: 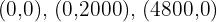 y el vértice
y el vértice 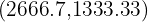 el cual se puede redondear al vértice
el cual se puede redondear al vértice 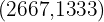 ya que las cantidades solo pueden ser números enteros positivos.
ya que las cantidades solo pueden ser números enteros positivos.
6 Calcular el valor de la función objetivo
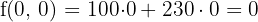 €
€
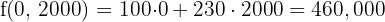 €
€
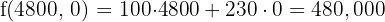 €
€
 € Máximo
€ Máximo
Con la producción y venta de 2667 baterías económicas y 1333 baterías de lujo, Julián obtendrá la máxima venta de 573,290€.
Siembra de maíz y cebada
9Un agricultor tiene 600 hectáreas en las que puede sembrar maíz o cebada y dispone de 800 horas de trabajo durante la temporada. Los márgenes de utilidad por hectárea para el maíz son de 60€ y para la cebada es de 70€. Los requerimientos laborales para trabajar en la siembra de maíz es de 1 hora por hectárea y en la siembra de cebada es de 2 horas por hectárea. ¿Cuántas hectáreas de cada cultivo debe sembrar para maximizar su utilidad?, ¿Cuál es la utilidad máxima?
1 Elección de las incógnitas.
 nº de hectáreas de maíz
nº de hectáreas de maíz
 nº de hectáreas de cebada
nº de hectáreas de cebada
2 Función objetivo

3 Restricciones
| Maíz | Cebada | Disponible | |
|---|---|---|---|
| Hectáreas | 1 | 1 | 600 |
| Horas | 1 | 2 | 800 |




4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.
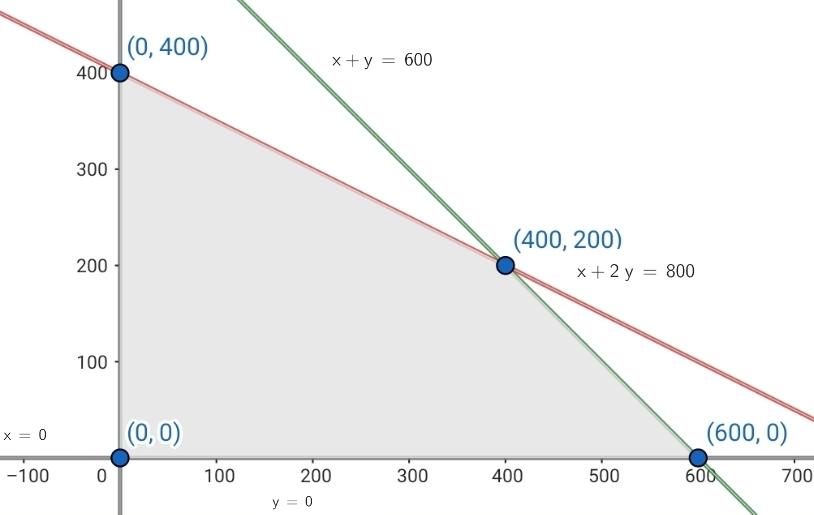
Los vértices son: 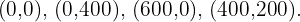
6 Calcular el valor de la función objetivo
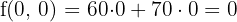 €
€
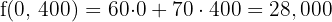 €
€
 €
€
 € Máximo
€ Máximo
El agricultor debe sembrar 400 hectáreas de maíz y 200 de cebada para obter la utilidad máxima de 38,000€.
¿Vives en la Ciudad Condal y buscas clases particulares matematicas? ¡Encuéntralas en Superprof!
Transporte de trabajadores
10Una empresa decide, por el día del trabajador, llevar de paseo a la playa a 400 trabajadores (por lo menos). Para ello contrata a una compañía de transporte, la cual dispone de autobuses para 60 pasajeros y microbuses para 20 pasajeros. El precio de alquiler de cada autobús es de 250€ y de cada microbús de 200€. La compañía de transporte solo dispone ese día de 8 choferes profesionales. ¿Qué número de autobuses y microbuses deben contratarse para que el costo sea mínimo?
1 Elección de las incógnitas.
 nº de autobuses
nº de autobuses
 nº de microbuses
nº de microbuses
2 Función objetivo

3 Restricciones
| Autobueses | Micobuses | Disponibles | |
|---|---|---|---|
| Pasajeros | 60 | 20 | 400 |
| Choferes | 1 | 1 | 8 |
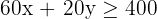
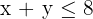


La primera desigualdad se debe a que al menos irán 400 empleados, pero podemos idear un plan de transporte en el que haya asientos disponibles siempre y cuando el coste sea el mínimo.
4 Hallar el conjunto de soluciones factibles

5 Calcular las coordenadas de los vértices del recinto de las soluciones factibles.

Los vértices son: 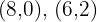 y el vértice
y el vértice 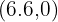 el cual se puede redondear al vértice
el cual se puede redondear al vértice 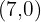 ya que las cantidades solo pueden ser números enteros positivos.
ya que las cantidades solo pueden ser números enteros positivos.
6 Calcular el valor de la función objetivo
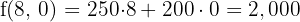 €
€
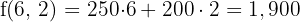 €
€
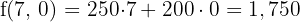 € Mínimo
€ Mínimo
Por lo tanto, con 7 autobuses con capacidad para 420 pasajeros la empresa gastará el mínimo de 1,750€
Si estás pensando que necesitas clases de matematicas, no dudes en entrar en Superprof, aquí encontrarás a los mejores profesionales, ya busques un profesor de matematicas online o uno presencial.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
LA EMPRESA “ABC” atiende los turistas que llegan diariamente. Esta dispone de los siguientes jugos: 150 litros de limón, 250 litros de parchita, 200 Litros de Naranja y 120 litros de Piña, la misma debe preparar dos mezclas con los jugos que vende que son: Jugo Coctel y Jugo de frutas. Considerando que la demandas siempre excede la existencia de la empresa y el resto de cada mezcla lo constituye un contenido muy barato.
El jugo Coctel debe contener por lo menos 15% de Jugo de limón 40% juga de piña y el jugo de frutas debe contener al menos 25% jugo de naranja, 30% de parchita y 20% de piña. Que rango de proporción se debe usar de cada jugo en las mezclas!? Defina las Variables de decisión respectivas
una. contadora elaborar formato de devolución de impuestos a personas físicas y pequeña empresa. en promedio de cada devolución a personas requiere de la contado y una hora de tiempo de computadora. cada devolución s empresa requiere cuatro horas de tiempo de la contadora 2 horas de la computadora debeido a otra consideración de la empresa el tiempo edta limitado a 240 horas y el tiempo de la computadora esta limitada a 100horas
6. Se van a fabricar dos tipos de juguetes, el primero requiere de 80 gramos de plástico y 5 gramos de pintura. El segundo necesita 60 gramos de plástico y 9 gramos de pintura. Esta semana contara 48 kg de plástico y 4.5 kg de pintura. ¿Cuántos juguetes de cada tipo se deben fabricar si la utilidad unitaria que dejan al negocio es de $6?00 y $7.00 respectivamente? y graficar
Supongamos que un operador turístico comienza con una inversión inicial de $5000 y cada mes aumenta su capital en una cantidad que depende del número de grupos turísticos que maneja. Cada grupo turístico genera un ingreso adicional de $…….. al mes
Una persona decide llevar un registro del gasto semanal en combustible para su automóvil. El costo del galón de combustible es de $3,pero cada vez que carga combustible tiene 2 galones en su tanque. Después de obtener los datos, represento la relación entre la cantidad de combustible y el gasto en una función afín y encuentra la ecuación de la función
Resuelve
Una señora ha pagado sólo 190 soles por una blusa y un pantalón, que entre los dos costaban 230 soles. Se sabe que le han rebajado 1 5 del precio de la blusa y 3 20 del precio original del pantalón. ¿Cuál era el precio original de cada prenda?
Una pastelería realiza dos tipos de torta, la imperial y la de chocolate.la función objetivo viene dada por la expresión:f(x,y)=8x+10y
Sujeto a: I)x+2y=0;y>=0
Se pide graficar, región solución factible y cantidad de cada tipo de torta para obtener el máximo objetivo
el municipio compró tres terrenos con áreas de 160,280 y480 hectáreas respectivamente los cuales se quieren dividir en lotes iguales con la mayor superficie posible para construir distintos proyectos de vivienda ¿ Cuál debe ser el área de estos lotes ?¿ Cuántos lotes salen de cada terreno
Una agencia de transportes tiene 10 sucursales en todo el país, que sumadas a la casa Central da un total de 11. La empresa posee un tipo de pasaje diferente para cada viaje, ya que cualquier pasajero puede trasladarse de cualquiera de las 11 ciudades a otra. ¿Cuántos tipos de pasajes diferentes se necesitarían tener para cubrir todas las posibilidades de compra de cada oficina?