Temas

Suma, multiplicación y potencia de matrices
Sean las matrices: 
Efectuar las siguientes operaciones:
1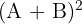
2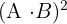
3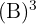
4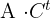
1 Para resolver, seguimos la jerarquía de operaciones, por lo cual primero sumamos las matrices:

Después, calculamos el cuadrado de la matriz:

Finalmente, mediante el desarrollando las operaciones obtenemos:

2 Para resolver este ejercicio, primero calculamos el producto de las matrices:

Después, calculamos el cuadrado del producto:

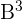 como
como 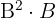 . Así bien como
. Así bien como 




Dimensión de matrices
Sean las matrices: 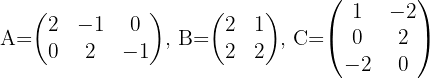 .
.
Para cada una de las siguientes expresiones, explique en que casos es posible calcular el producto y en cuales no.
1 
2 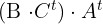
3 Determina la dimensión de  para que pueda efectuarse el producto
para que pueda efectuarse el producto 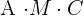
4 Determina la dimensión de  para que
para que  sea una matriz cuadrada.
sea una matriz cuadrada.
¿Buscas clases algebra lineal? ¡Encuéntralas en Superprof!
Antes de plantear las soluciones es importante destacar que la notación sobre la dimensión de una matriz  constituida por
constituida por  filas y
filas y  columnas se denota de la siguiente manera:
columnas se denota de la siguiente manera:  .
.
Además, para poder efectuar la multiplicación de dos matrices, se debe satisfacer que: El número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz (con la particularidad de que la matriz obtenida del producto tendrá el mismo número de filas que la primera matriz y el mismo número de columnas que la segunda matriz).
 debemos analizar las dimensiones de cada una de las matrices involucradas:
debemos analizar las dimensiones de cada una de las matrices involucradas: es una matriz de dimensión
es una matriz de dimensión  por lo que
por lo que  es
es 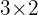 .
. es una matriz de dimensión
es una matriz de dimensión  .
. es una matriz de dimensión
es una matriz de dimensión 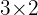 .
.Así bien podemos expresar lo anterior de la siguiente manera:
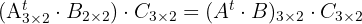
Notemos que como el numero de columnas de 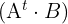 no coincide con el número de filas de
no coincide con el número de filas de  por lo cual la operación no puede ser efectuada.
por lo cual la operación no puede ser efectuada.
2 
Notemos que:
 es una matriz de dimensión
es una matriz de dimensión 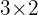 .
.
 es una matriz de dimensión
es una matriz de dimensión  .
.
 es una matriz de dimensión
es una matriz de dimensión 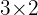 por lo que
por lo que 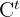 es de dimensión
es de dimensión  .
.
Podemos reescribir:

 .
.  para que pueda efectuarse el producto
para que pueda efectuarse el producto 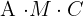
Recordemos que para poder multiplicar dos matrices es necesario que el número de columnas de la primera matriz sea igual al número de filas de la segunda,  es una matriz de dimensión
es una matriz de dimensión  , es decir dos filas y tres columnas entonces
, es decir dos filas y tres columnas entonces  debe de tener tres filas, es decir
debe de tener tres filas, es decir 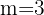
4 Determina la dimensión de  para que
para que 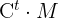 sea una matriz cuadrada.
sea una matriz cuadrada.
La matriz  tiene de dimensión
tiene de dimensión 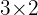 por tanto su traspuesta tiene de dimensión
por tanto su traspuesta tiene de dimensión  , para poder multiplicarla por
, para poder multiplicarla por  el número de columnas de
el número de columnas de 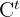 tiene que coincidir con el número de filas de
tiene que coincidir con el número de filas de  , es decir que
, es decir que 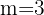 .
.
El producto de 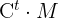 es una matriz con el mismo número de filas que
es una matriz con el mismo número de filas que 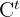 es decir
es decir  y el mismo número de columnas que
y el mismo número de columnas que  . Por ser el producto una matriz cuadrada el número de columnas de
. Por ser el producto una matriz cuadrada el número de columnas de  tiene que ser también 2.Entonces la matriz
tiene que ser también 2.Entonces la matriz  tiene de dimensión
tiene de dimensión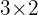 .
.
Conmutación de matrices
Calcular todas las matrices que conmuten con la matriz: 
Recordemos que para que dos matrices conmuten deben de satisfacer que  . Si consideramos
. Si consideramos 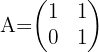 y
y 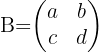 , tenemos la siguiente igualdad:
, tenemos la siguiente igualdad:
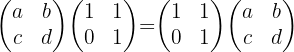
Desarrollando en ambos lados de la desigualdad obtenemos:
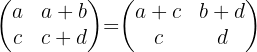
De lo anterior se deducen las siguientes igualdades:

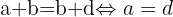


Por lo cual la matriz debe de ser de la forma 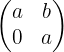
Ecuaciones matriciales
Sea 
Resolver la ecuación matricial
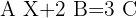
Para calcular el valor de  es necesario aplicar operaciones en ambos lados de la igualdad. Primero restamos en ambos lados
es necesario aplicar operaciones en ambos lados de la igualdad. Primero restamos en ambos lados  y luego multiplicamos por la matriz inversa de
y luego multiplicamos por la matriz inversa de  como se muestra a continuación:
como se muestra a continuación:
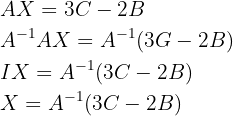
Una vez que tenemos expresada la solución, calculamos la matriz inversa de  :
:
 .
.
Finalmente, sustituimos y desarrollamos:

Problema de matrices contextualizado
Una empresa de muebles fabrica tres modelos de estanterías: A, B y C. En cada uno de los tamaños, grande y pequeño. Produce diariamente 1000 estanterías grandes y 8000 pequeñas de tipo A, 8000 grandes y 6000 pequeñas de tipo B, y 4000 grandes y 6000 pequeñas de tipo C. Cada estantería grande lleva 16 tornillos y 6 soportes, y cada estantería pequeña lleva 12 tornillos y 4 soportes, en cualquiera de los tres modelos.
1 Representar esta información en dos matrices.
2 Hallar una matriz que represente la cantidad de tornillos y de soportes necesarios para la producción diaria de cada uno de los seis modelos−tamaño de estantería.
Filas: Modelos A, B, C Columnas: Tipos G, P

Matriz de los elementos de las estanterías:
Filas: Tipos G, P Columnas: T, S

2 Hallar una matriz que represente la cantidad de tornillos y de soportes necesarios para la producción diaria de cada uno de los seis modelos−tamaño de estantería.
Matriz que expresa el número de tornillos y soportes para cada modelo de estantería:
Filas: Modelos A, B, C Columnas: Tipos T, S














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Funcion inversa de
b=f(x)=x-7/3
Hola, en ecuaciones matriciales, en el ejercicio 4, los valores de B y de C están intercambiados en la solución
Ya lo revise y no veo lo que mencionas. La matriz C solo se usa para la multiplicación con la suma de la inversa de A y B.
Buenas, parece haber un error en el ejercicio 3 , de AX=B: A=[1 3][1 4] y B=[1 -1][3 1], porque la respuesta que ustedes dan es: X=[1 -5][0 4], y a mi me da: X=[-5 -7][2 2], no se si es error mío o suyo, ya que lo confirmé con calculadora externa y mi respuesta está bien.
𝐴 =
[2 −1
3 1]
Una disculpa ya se corrigió.
8(3 * 7) matrix ]-\ (3*(4*-12)\ +16*(2-978
Cuales son los pasos para resolver una ecuacion x matrices y escribe sus fórmulas
2x-z=14
4x+y-z=41
3x-y+5x=53