Chapters
In this article, we will discuss how to divide polynomials using Ruffini's rule.
Introduction
You may be familiar with a general long division of a polynomial by its factor. This method is generally used to divide the polynomials. However, there is another method for dividing the polynomial by a factor of the form x - a which is an alternative of long division. This method is known as Ruffini's rule. This rule works by reducing both the polynomial and its factor into a set of numbers. After analyzing these values, the resulting set of numbers are used to yield the quotient and the remainder. The divisor in Ruffini's rule is a linear factor of the polynomial, therefore, we can say that this rule is a special case of synthetic long division.
A Ruffini's rule is used to:
- Divide the equations of third-degree or higher. The degree of an equation means the highest power any variable has in that equation. If an equation is a third-degree polynomial, then it means that the highest degree of a variable in that equation will be 3.
- Find the factors of the third degree or higher polynomials
- Compute the roots or zeroes of the third degree or higher polynomials
In the next section, we will solve some examples step by step that will clarify this rule further.
Example 1
Use Ruffini's rule to perform the following division:
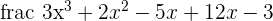
Solution
Follow these steps to perform the long division using Ruffini's method.
Step 1
In this step, you need to write down the coefficients of the dividend horizontally and the root of the divisor on the left side. To find the root, set the divisor equal to 0 like this:
The coefficients of the dividend 
are 3 , 2, -5 and 12. The root of the divisor is 3.
Step 2
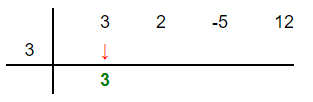
Step 3
Now, we will multiply the root of the divisor by 3 to get 9 and put this 9 in the second column as shown below:
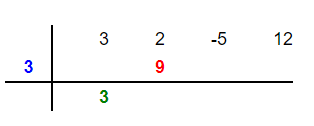
Step 4
Add the new number 9 and the coefficient 2 to get 11. Place this number 11 below these two numbers in the second column as shown below:
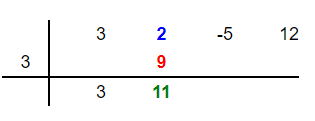
Step 5
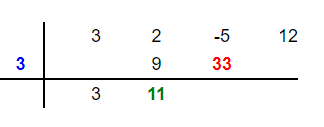
Step 6
Vertically add -5 and 33 to get 28. Place 28 below these two numbers in the third column as shown below:
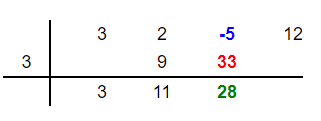
Step 7
Multiply the root 3 by the new number 28 to get 84. Place this number 84 in the fourth column below 12 like this:
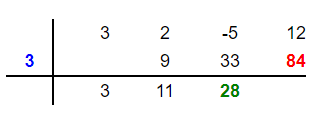
Step 8
Add 12 and 84 to get 96 and place this number in the fourth column below these two numbers as shown below:
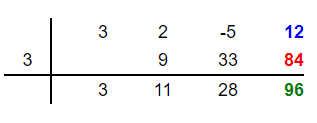
Our division is complete now. The entries in the result row have formed a new equation that has one degree less than the original polynomial. This new equation is 
. The last digit 96 is not zero, so this is a remainder. Finally, we can write the answer as:
Quotient =
Remainder = 96
Find more Maths tutor here on Superprof.
Example 2
Use Ruffini's rule to perform the following division:
Solution
Before starting to solve the above polynomial using Ruffini's method, first, you need to identify the missing power from the dividend and write its coefficient 0. The polynomial in this example has missing power 3 because after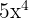 
, we see 
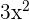directly. Hence, we will write the polynomial as 
.
Step 1
In this step, you need to write down the coefficients of the dividend horizontally and the root of the divisor on the left side. To find the root, set the divisor equal to 0 like this:
The coefficients of the dividend are 5 , 0, 3 , -2 and 11. The root of the divisor is -2.
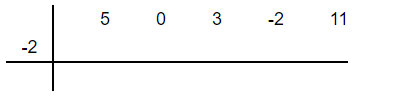
Step 2
In this step, we will bring the first coefficient down as it is. In this example, we will bring down 5 as shown below:
Step 3
Now, we will multiply the root of the divisor which is -2 in this example by 5 to get -10 and put this -10 in the second column as shown below:
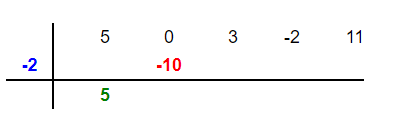
Step 4
Add the new number -10 and the coefficient 0 to get -10. Place this number -10 below these two numbers in the second column as shown below:
Step 5
Multiply the root -2 with the last number -10 to get 20. Place this number 20 in the third column below the third coefficient 3 as shown below:
Step 6
Vertically add 3 and 20 to get 23. Place 23 below these two numbers in the third column as shown below:
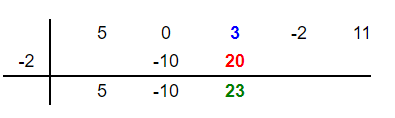
Step 7
Multiply the root -2 by the new number 23 to get -46. Place this number -46 in the fourth column below -2 like this:
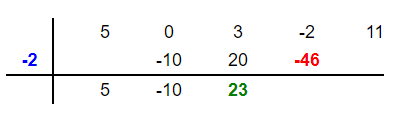
Step 8
Add -46 and -2 to get -48 and place this number in the fourth column below these two numbers as shown below:
Step 9
Multiply -2 by -48 to get 96 and put it in the fifth column below 11 like this:
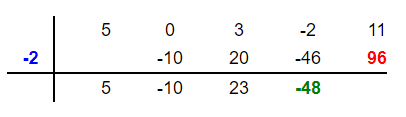
Step 10
Add 11 and 96 to get 107 and place it below 96 in the fifth column as shown below:
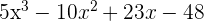. The last digit 107 is not zero, so this is a remainder. Finally, we can write the answer as: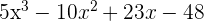
Example 3
Use Ruffini's rule to perform the following division:
Solution
Follow these steps to perform the long division using Ruffini's method.
Step 1
In this step, you need to write down the coefficients of the dividend horizontally and the root of the divisor on the left side. To find the root, set the divisor equal to 0 like this:
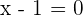
The coefficients of the dividend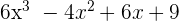 
are 6, -4, 6 and 9. The root of the divisor is 1.
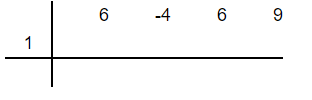
Step 2
In this step, we will bring the first coefficient down as it is. In this example, we will bring down 6 as shown below:
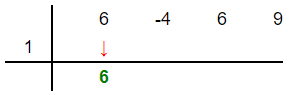
Step 3
Now, we will multiply the root of the divisor which is 1 in this example by 6 to get 6 and put this 6 in the second column as shown below:
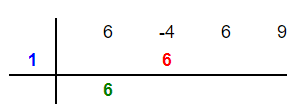
Step 4
Add the new number 6 and the coefficient -4 to get 2. Place this number 2 below these two numbers in the second column as shown below:
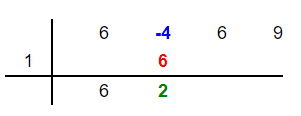
Step 5
Multiply the root 1 with the last number 2 to get 2. Place this 2 in the third column below the third coefficient 6 as shown below:
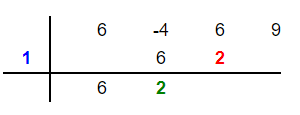
Step 6
Vertically add 2 and 6 to get 8. Place 8 below these two numbers in the third column as shown below:
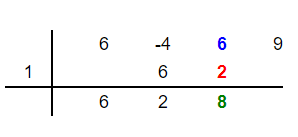
Step 7
Multiply the root 1 by the new number 8 to get 8. Place this number 8 in the fourth column below 9 like this:
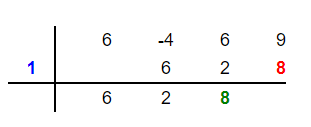
Step 8
Add 8 and 9 to get 17 and place this number in the fourth column below these two numbers as shown below:
Our division is complete now. The entries in the result row have formed a new equation that is one degree lesser than the original polynomial. This new equation is 
. The last digit 17 is not zero, so this is a remainder. Finally, we can write the answer as:
Quotient =
Remainder = 17
Did you like this article? Rate it!
Loading...
