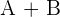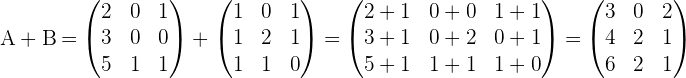Adding matrices is very easy unlike multiplication of matrices(which is very complicated). If you know how to perform an addition operation of two or more than two numbers then you won't have much problem in this lesson.
Given two matrices of the same dimension, 
and 
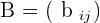, the matrix sum is defined as: 
. That is, the resultant matrix's elements are obtained by adding the elements of the two matrices that occupy the same position. Let's break it down in simple words, for example, you have two matrices,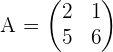 
and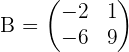 
, the first thing you should see is the dimension of both matrices. The dimension of matrix A is 
, however, the dimension of the matrix B is as well. There is one condition if you want to add two or more two matrices. All the matrices should have the SAME dimensions. It means all the matrices should have equal number of rows as well as equal number of columns. If they have an equal number of rows and columns that means they all have the same dimension. In the case of the above example, matrices A and B have the same dimension because they have the equal number of rows and columns.
Once the condition is valid, the next step is to add the elements of the matrices. To add those elements, you need to pick an element of a matrix and then add it in the same position to the element of another matrix, for example, we picked matrix A and selected the element 
. To add that , we went to another matrix(which is B) and at the same position, we selected the element(which is 
). Now apply the addition operation and then place it in a new matrix. Do this to all the other elements of the matrix in the same way.
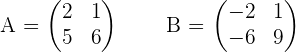
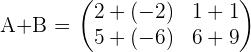
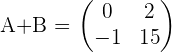
Properties of the Addition of Matrices
There are some properties of adding matrices that you should know. Below are all the properties:
Property No.1: Closure
This property tells that if you add two matrices(of dimension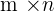 
) this will result in a new matrix of the same dimension(which is ).
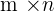Property No.2: Associative
It doesn't matter what way you group, it will always result in the same. In simple words, the way in which the addends are grouped does not change the result.
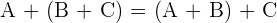
Property No.3: Additive Identity
Adding a zero matrix(of the same dimension) will not change the overall result. If you add a zero matrix to any matrix, it will always result in the same matrix.
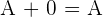
Where 
is the zero matrix of the same dimension.
Property No.4: Additive Inverse
If you add two matrices with the same elements and dimension but with opposite signs will always result in zero.
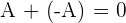
The opposite matrix has each of its elements change sign.
Property No.5: Commutative
When you are adding two matrices, the order doesn't change the sum.
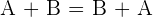
Example
Given the matrices:
Calculate:
Did you like this article? Rate it!
Loading...
