Common Algebraic Expressions
The double of a number: 
The triple of a number: 
The quadruple of a number: 
Half of a number: 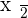
A third of a number: 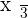
A quarter of a number: 
A number is proportional to 
A number to the square: 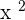
A number to the cube: 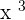
Two consecutive numbers:  and
and  .
.
Two consecutive even numbers:  and
and 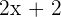 .
.
Two consecutive odd numbers:  and
and  .
.
Break  in two parts:
in two parts:  and
and 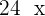 .
.
The sum of the two numbers will be  .
.
The difference between the two numbers will be  .
.
The product of the two numbers will be  .
.
The quotient of the two numbers will be  .
.
Age Word Problems
 and his son,
and his son,  . After how many years is the father's age three times greater than the age of his son?
. After how many years is the father's age three times greater than the age of his son? Let the number of years = 


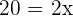
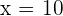
After 10 years.
Find a maths tutor on Superprof.
Q. Today, John is three-quarters the age of his father and the difference in age is 15 years. Four years ago, the age of the father was twice the age of John. Find the age of the father and son 4 years ago.
| John | Father of John | |
|---|---|---|
| Four years ago |  |  |
| Today |  | 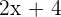 |
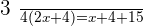

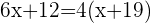
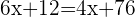
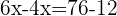
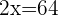
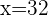
Age of John: 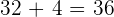 .
.
Age or father:  .
.
Work Word Problems
Q. Working together, it takes two workers 14 hours to complete a task. How long does it take to do the same task separately if one worker is twice as fast as the other?
| Fast | Slow | |
|---|---|---|
| Time |  |  |
| Hours | 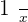 |  |


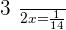
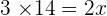
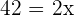
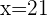
For the slow worker=
Number Word Problems
Q. If the double of a number is subtracted by its half and the result is 54. What is the number?
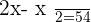
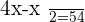

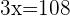

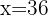
Q. There is a two-digit number and the digits that form it are consecutively ordered. The greater digit is in the first figure that forms the number (to the left) and the smaller digit is the second figure. The number equals six times the sum of its figures. What is the number?
Units (second figure)
Tens(first figure)
If there is a two-digit number, for example,  , it can be broken down, as follows:
, it can be broken down, as follows:  .
.
The two-digit number is 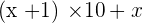 .
.
As this number is six times greater than the sum of its figures:  , then:
, then:

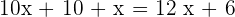



Units 
Tens 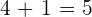
Number 
Geometric Word Problems
Q. Find the value of the three angles in a triangle knowing that Angle B is 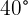 greater than Angle C and A is
greater than Angle C and A is 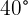 greater than B.
greater than B.

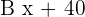

The three angles measure 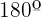 .
.

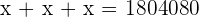
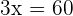
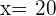
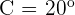
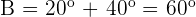

Q. The base of a rectangle is twice its height. What are its dimensions if the perimeter is 30 cm?
Height 
Base 
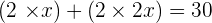
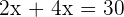
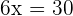

Height 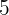
Base 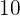
Mixture Word Problems
Q. A trader has two types of coffee, the first is  dollars/kg, and the second,
dollars/kg, and the second,  dollars/kg.
dollars/kg.
How many kilograms of each type of coffee must be mixed together to get  kilograms of a mixture that would cost
kilograms of a mixture that would cost  dollars/kg?
dollars/kg?
| 1st Type | 2nd Type | Total | |
|---|---|---|---|
| Number of kg |  | 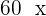 |  |
| Value | 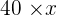 |  | 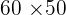 |
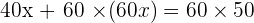

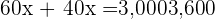
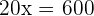
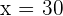
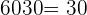
The mix is 30 kilograms of the 1st type and 30 of the 2nd type
Q. There are two different types of silver and each type is divided into portions of one gram. The first type is  purity and the other of
purity and the other of 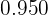 purity. What is the weight of a bar that is formed by the contents of both types to obtain
purity. What is the weight of a bar that is formed by the contents of both types to obtain  grams of silver at
grams of silver at  purity?
purity?
| 1st Type | 2nd Type | Total | |
|---|---|---|---|
| No. of g |  | 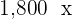 |  |
| Silver | 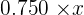 | 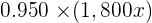 | 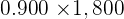 |
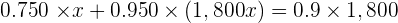
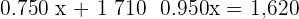
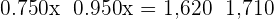
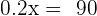
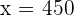
1st type  grams
grams
2nd type 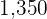 grams
grams
Boost your learning speed and understanding with a maths tutor on Superprof.



3^x -2^y+2=10
2^x-3^x-2=2