¡Bienvenidos a nuestra página de ejercicios de Trigonometría! Aquí encontrarás una amplia gama de problemas que abarcan desde lo más básico hasta los conceptos más avanzados de este fascinante campo de las matemáticas.
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de los triángulos. Con raíces antiguas en la astronomía y la navegación, esta disciplina tiene aplicaciones en una variedad de campos, desde la física hasta la ingeniería, pasando por la informática y mucho más.
Nuestra página está diseñada para ayudarte a fortalecer tus habilidades en trigonometría, Cada ejercicio está diseñado para desafiar tu comprensión y mejorar tus habilidades de resolución de problemas.
Recuerda, la práctica hace al maestro. Así que, ¡adelante! Sumérgete en estos ejercicios y descubre la belleza y la utilidad de la trigonometría.
1 Sabiendo que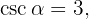 
calcular las restantes razones trigonométricas.
y 
serán los mismos valores para ambos cuadrantes, la diferencia entre los casos son los signos de algunas razones trigonométricas. Entonces comenzamos por encontrar los valores de y .La definición de la cosecante es 
, por lo tanto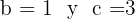 
, ahora calculamos el valor de 
usando pitágoras,
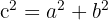
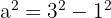
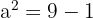
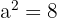
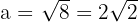
En este cuadrante todas las razones trigonométricas son positivas:
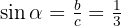
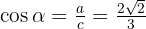
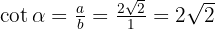
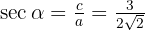
En este cuadrante algunas razones trigonométricas tienen signo negativo, ya que el valor de
en este cuadrante es negativo: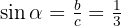 
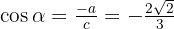
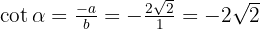
2 Calcula las razones de los siguientes ángulos:
a 
b 
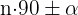dónde si 
es par entonces es igual a la función de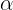 
, es decir,
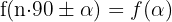, donde 
representa a las funciones trigonométricas.También es importante recordar que las funciones tienen diferentes signos dependiendo del cuadrante en el que se encuentren.
a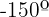
Vamos a calcular las funciones trigonométricas, observemos que 
entonces estamos en el cuadrante II, por lo tanto tenemos que considerar el signo de cada una de las funciones,
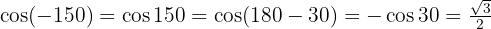
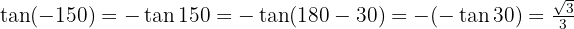
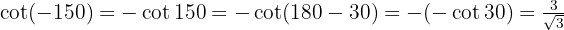
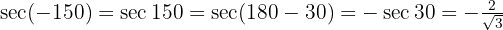
b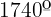
Seguimos teniendo un ángulo mayor que 90º, de hecho es más grande que 360º, por lo tanto comenzamos por dividir el ángulo entre 360, para encontrar su equivalente:
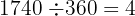y tenemos un residuo de 
, el cual es el equivalente, por lo tanto calcularemos las funciones trigonométricas para el ángulo .
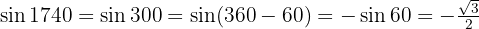
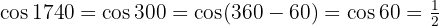
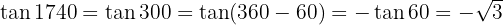
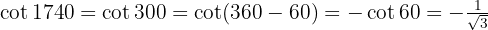
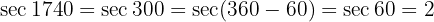
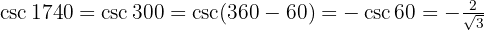
3 Simplificar las fracciones:
a 
b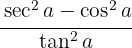 
c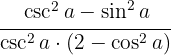 
a
Comenzaremos aplicando directamente las correspondientes identidades trigonométricas y posteriormente cambiamos la definición de secante y cosecante,
Para finalmente hacer la división de fracciones y encontrar la definición de tangente.
b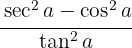
Comenzamos por usar la definición de secante, hacer la resta y división de fracciones,
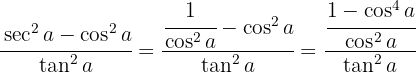
Convertimos la diferencia de cuadrados en binomios conjugados y cambiamos la definición de tangente.
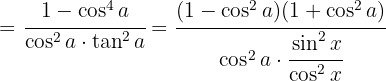
Se cancelan los cosenos y usamos la identidad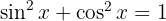 
c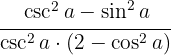
Comenzamos por separar las fracciones y simplificar,
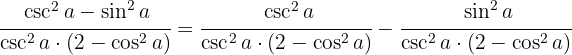
Volvemos a juntar la resta y separamos el número 2 para poder usar la identidad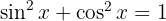
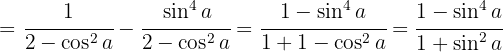
Convertimos la diferencia de cuadrados en binomios conjugados y volvemos a aplicar la identidad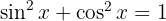
4Calcular la longitud del lado y de la apotema de un octógono regular inscrito en una circunferencia de 49 centímetros de radio.
Comenzamos por calcular el valor del ángulo,
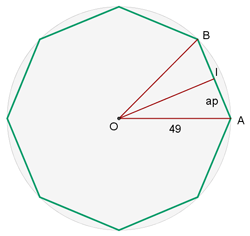
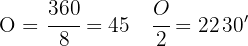
Dividimos el ángulo a la mitad para poder formar un triángulo rectángulo y así poder aplicar las funciones trigonométricas.Para encontrar el valor del lado usamos la función seno.
Entonces despejando el valor de l, tenemos: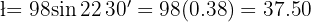
cmPara encontrar el valor del apotema usamos la función coseno.
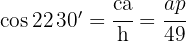Despejamos el apotema,
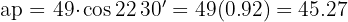cm5 Tres pueblos A, B y C están unidos por carreteras. La distancia de A a C es 6 km y la de B a C 9 km. El ángulo que forman estas carreteras es 120°. ¿Cuánto distan A y B?
Para encontrar el valor de la distancia que hay entre A y B la forma más sencilla es aplicar la ley de cosenos,
Comenzamos por aplicar directamente la ley de cosenos, es decir:
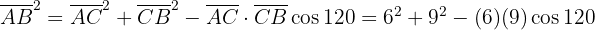
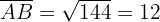cm
6 Resuelve la siguiente ecuación trigonométrica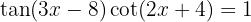 
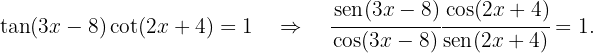
Si quitamos denominadores y pasamos restando el término de la derecha, obtenemos
Ahora, usamos la fórmula para la resta de ángulos de la función seno
para obtener que
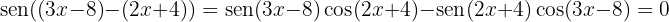
Por lo tanto, obtenemos que
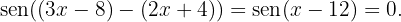
Así, el problema se reduce a resolver la ecuación
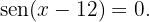
Recordemos que, la función seno se anula cuando su argumento es un múltiplo entero de
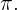Así, obtenemos que
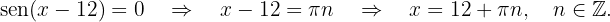Por lo tanto, la solución es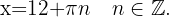 
7 Obtén el valor de lo siguiente
a 
b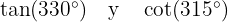 
c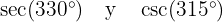 
donde 
es un número par y 
representa a cualquiera de las funciones trigonométricas. a
Usando el resultado de arriba con 
tenemos que
b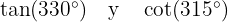
Usando la definición de tangente en términos de la función seno y coseno tenemos que
donde hemos usado el primer inciso para obtener el resultado.
Ahora usamos la definición de cotangente en términos de seno y coseno
c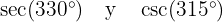
Para resolver esto usamos las identidades
Por lo tanto
8 Utilizando que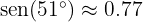 
, hallar el valor de 
en la siguiente imagen
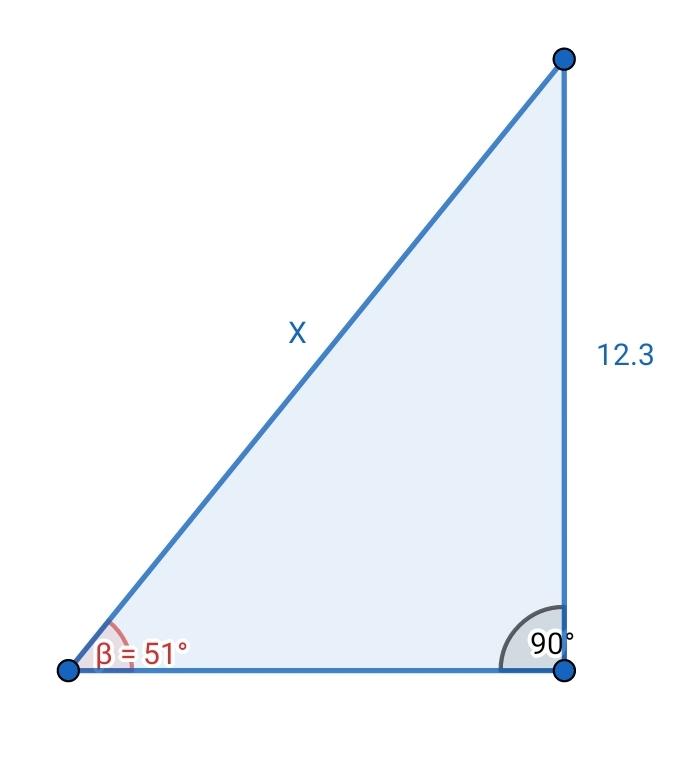
representa la hipotenusa del triángulo rectángulo de la imagen. Tenemos información del ángulo y del cateto opuesto al ángulo, por lo tanto, como queremos conocer la hipotenusa, utilizamos la función seno: 
Por lo tanto, se tiene que
Así, se tiene finalmente que
9 Demuestra las siguientes identidades trigonométricas
b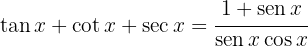 
a
Observe que
donde hemos utilizado la identidad 
b 
Observe que
10 Resuelve las siguientes ecuaciones trigonométricas
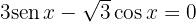en el intervalo 
b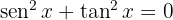 
en el intervalo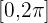 
a 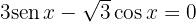en el intervalo
Tenemos que
Así,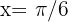 
es la única solución en el intervalo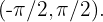 
b 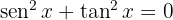en el intervalo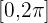
Observe que
Lo anterior implica que
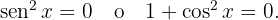
- Si
- Si
la cual no tiene soluciones reales.
Por lo tanto, la solución es
En el intervalo 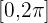, las soluciones son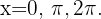 
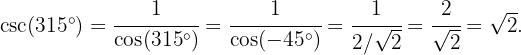
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
C=49 A=54 a=72
b = 40,2 a = 31, 5 B = 112 °20
Encontrar la solucion principal de la ecuación trigonometría asenX+bcosX = cl donde a, b y c son numeros reales y a≠0, b≠0
Ayúdeme en éste ejercicio por favor.
Complete el siguiente triángulo rectangulo, calculando sus ángulos en cada unos de los vértices:
* Ángulo del vértice (A) es alpha, y su dimensión es 7
* Hipotenusa es b.
* Ángulo del vértice (C) es beta, y su dimensión es raíz de 5.
Demostrar que los ángulos del triángulo es 90°, aplicando cada uno de los procesos.
Muy amable, gracias 🫂
Sj dos lados de un triangulo miden 200m y 18cm y el angulo comprendido, entre ello Calcular el área def trianguts
Lucy ayúdeme en este trabajo
Seno=30÷c
Resolver los siguientes Triángulos Oblicuángulos, aplicando las Leyes
del Seno, Coseno y/o Tangente:
o a = 41; b = 19,5; c= 32,48
o a=5,312; b = 10,913; c = 13
o a = 32,45; b = 27,21; C = 66° 56′
b = 50; c = 66,6; A = 83° 26′
o a=41; B = 27°50′; C = 51°
O
a= 78,6; A = 83°26′; B = 39°13′
me pueden ayudar es urgente