Temas
Estudia la monotonía, la convergencia o divergencia y las cotas de las sucesiones
1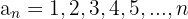
2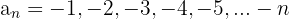
3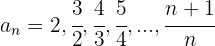
4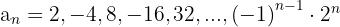
5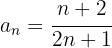
6
7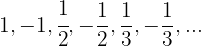
8
Estudia la monotonía, la convergencia o divergencia y las cotas de las sucesiones
Soluciones:
1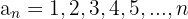
Es creciente
Está acotada inferiormente
Cotas inferiores: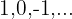 
El mínimo es 
No está acotada superiormente
Divergente
2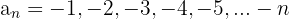
Es decreciente
Está acotada superiormente
Cotas superiores: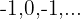 
El máximo es 
No está acotada inferiormente
Divergente
3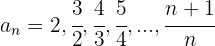
Es decreciente
Está acotada superiormente
Cotas superiores: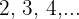 
El máximo es 
Está acotada inferiormente
Cotas inferiores: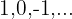
El ínfimo es
Convergente,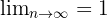 
4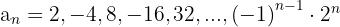
No es monótona
No está acotada
No es convergente ni divergente
5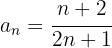
Los primeros términos de esta sucesión son:
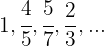
Es monótona estrictamente decreciente
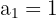
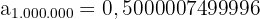
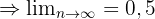
Nuestro profesor matematicas puede ayudarte.
Sucesión convergente
Por ser decreciente, es una cota superior, el máximo.
es una cota inferior, el ínfimo o extremo inferior.
Por tanto la sucesión está acotada
6
Los primeros términos de la sucesión son:
No es monótona
No es convergente ni divergente
No está acotada
7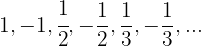
No es monótona
Es convergente porque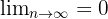 
Está acotada superiormente, es el máximo
Está acotada inferiormente, es el mínimo
Está acotada
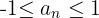
8
Los primeros términos de la sucesión son:
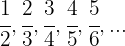
Es monotona estrictamente creciente
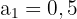
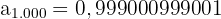
Sucesión convergente
Está acotada inferiormente, 
es el mínimo
Está acotada superiormente. es el supremo
Por tanto la sucesión está acotada
Hallar el término general de las siguientes sucesiones
1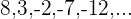
2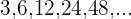
3
4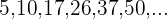
5
6
7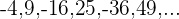
8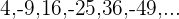
9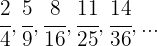
10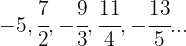
Hallar el término general de las siguientes sucesiones
1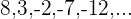
Podemos obtener la diferencia entre los términos consecutivos:
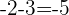
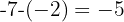
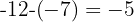
Debido a que la diferencia es constante,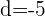 
Es una progresión aritmética
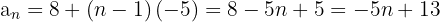
2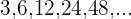
Podemos dividir cada termino por su antecesor:
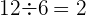
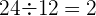
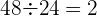
Como el cociente es constante, 
se trata de una progresión geométrica
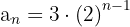
3
La sucesión se puede reescribir como:
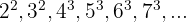
Observamos que las bases están en progresión aritmética, siendo 
, y el exponente es constante, por lo que podemos escribir la siguiente sucesión para la base:
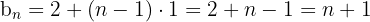
Por lo que el término general es:
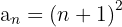
4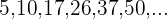
Cada término de esta sucesión es el consecutivo de los términos de la sucesión anterior, por lo que podemos reescribirla como:
Hallamos el término general como vimos en el caso anterior y le sumamos 1.
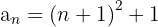
5
La sucesión se puede reescribir como:
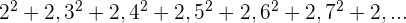
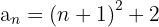
6
La sucesión se puede reescribir como:
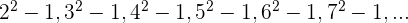
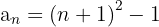
7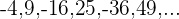
Cada uno de los términos de esta sucesión es el inverso de cada uno de los términos de la sucesión 
, por lo que:
8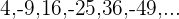
9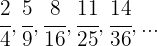
Tenemos dos sucesiones, una para el numerado y otra para el denominador:
La primera es una progresión aritmética con 
, la segunda es una sucesión de cuadrados perfectos.
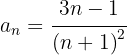
10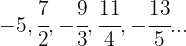
Si prescindimos del signo, el numerador es una progresión aritmética con una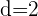 
.
El denominador es una progresión aritmética de .
Por ser los términos impares los negativos multiplicamos por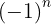 
.
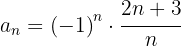
Calcular el término general de las siguientes sucesiones
1
2
3
4
5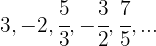
6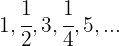
7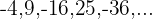
8
9
10
Calcular el término general de las siguientes sucesiones:
Soluciones:
1
El numerador es constante.
El denominador es una progresión aritmética de .
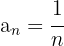
2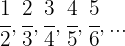
El numerador es una progresión aritmética con una
El denominador es una progresión aritmética con una
3
Si escribimos cada término de la sucesión en forma racional, obtendríamos:
El numerador es una progresión aritmética con una
El denominador es una progresión aritmética de
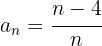
4
Si prescindimos del signo es una progresión aritmética con una
Por ser los términos impares los negativos multiplicamos por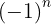
5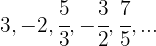
La sucesión puede reescribirse como:
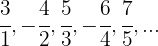
Si prescindimos del signo, el numerador es una progresión aritmética con una
El denominador es una progresión aritmética de
Por ser los términos pares los negativos multiplicamos por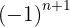 
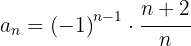
6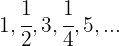
Es una sucesión oscilante
Los términos impares forman progresión aritmética con una , si no tenemos en cuenta los términos pares
El denominador de los términos pares forman progresión aritmética con una
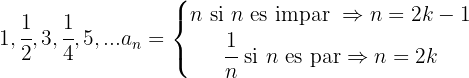
7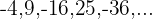
La sucesión se puede reescribir
Si prescindimos del signo y del exponente tenemos una progresión aritmética con una
Por estar los términos al cuadrado, tenemos que elevar el término general al cuadrado
Por ser los términos impares los negativos multiplicamos por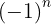
8
La sucesión se puede reescribir como:
Es una sucesión oscilante
El numerador de los términos impares forman progresión aritmética con una , si no tenemos en cuenta los términos pares.
Por estar los términos al cuadrado, tenemos que elevar el término general al cuadrado
El primer sumando del denominador (prescindiendo del cuadrado) es una progresión aritmética de (sin contar los términos pares)
El término general lo tenemos que elevar al cuadrado y sumarle
Los términos pares forman una sucesión constante.
9
Separando las sucesiones del numerador y el denominador tenemos:
Numerador: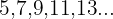 
Denominador: 
El numerador es una progresión aritmética con una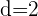
El denominador es una progresión geométrica con una
10
Si prescindimos del signo, el numerador es una progresión aritmética con una
El denominador es una progresión geométrica con una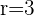 
Por ser los términos pares los negativos multiplicamos por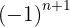
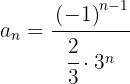
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma.de los 9 primeros términos de una progresión es 219, si el primer término de la progresión es -4, habllar el último término An.
Son todos los tiempos de sucesiones?
No es clara tu pregunta, si te refieres a los ejercicios de inversión y depende del problema planteado.
Tres números x y z forman una progresión geométrica creciente que cumple x + y + z = 21 y x por y por z = 2 16 determina la razón de la progresión dada
Cuál es el número de término de una progresión aritmética cuando la diferencia común de los términos en 5,el primer término es 1 y el último es 46
En una PG a9 =56yr =1 , hallar a6
2
Encuentra el 6to,8vo,10mo termino de la siguiente sucesión geometrica3,6,12,14
Una progresión geométrica de razón positiva consta de 4 terminos
Porfa alguien me puede ayudar a comprender como puedo resolver un ejercisio sobre Sumar todos los términos de la progresión
1,34, 916, 2764, … y ando mas perdidaa