 .
.
1 Comprobar si la sucesión 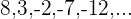 es una progresión aritmética.
es una progresión aritmética.

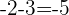


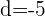
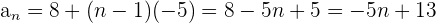
2 Comprobar si la sucesión 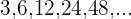 es una progresión geométrica.
es una progresión geométrica.

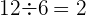
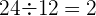
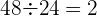

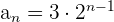
3 Comprobar si los términos de la sucesión  son cuadrados perfectos.
son cuadrados perfectos.

Observamos que las bases están en progresión aritmética, siendo  , y el exponente es constante
, y el exponente es constante

Por lo que el término general es:

También nos podemos encontrar con sucesiones cuyos términos son números próximos a cuadrados perfectos
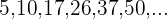

Hallamos el término general como vimos en el ejemplo anterior y le sumamos 1.
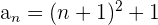

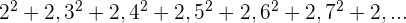
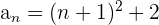

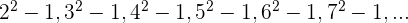
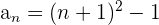
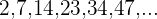
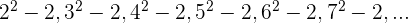
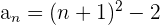
4 Si los términos de la sucesión cambian consecutivamente de signo.
Si los términos impares son negativos y los pares positivos: Multiplicamos  por
por  .
.
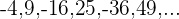

Si los términos impares son positivos y los pares negativos: Multiplicamos  por
por  .
.
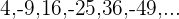
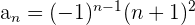
5 Si los términos de la sucesión son fraccionarios (no siendo una progresión).
Se calcula el término general del numerador y denominador por separado.

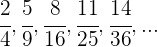
Tenemos dos sucesiones:


La primera es una progresión aritmética con  , la segunda es una sucesión de cuadrados perfectos
, la segunda es una sucesión de cuadrados perfectos
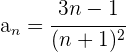



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La suma.de los 9 primeros términos de una progresión es 219, si el primer término de la progresión es -4, habllar el último término An.
Son todos los tiempos de sucesiones?
No es clara tu pregunta, si te refieres a los ejercicios de inversión y depende del problema planteado.
Tres números x y z forman una progresión geométrica creciente que cumple x + y + z = 21 y x por y por z = 2 16 determina la razón de la progresión dada
Cuál es el número de término de una progresión aritmética cuando la diferencia común de los términos en 5,el primer término es 1 y el último es 46
En una PG a9 =56yr =1 , hallar a6
2
Encuentra el 6to,8vo,10mo termino de la siguiente sucesión geometrica3,6,12,14
Una progresión geométrica de razón positiva consta de 4 terminos
Porfa alguien me puede ayudar a comprender como puedo resolver un ejercisio sobre Sumar todos los términos de la progresión
1,34, 916, 2764, … y ando mas perdidaa