Una ecuación exponencial es aquella ecuación en la que la incógnita aparece en el exponente.
Para resolver una ecuación exponencial vamos a tener en cuenta:
Las propiedades de las potencias
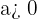
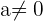
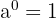
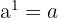
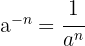
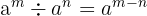
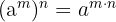
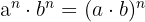
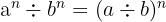
- si
entonces 
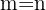
Resolución de ecuaciones exponenciales
Caso 1:Ambos miembros pueden expresarse en la misma base
Realizar las operaciones necesarias para que en los miembros tengamos la misma base, de modo que podemos igualar los exponentes.
Ejemplos
1 
Reescribimos el lado derecho como 
y descomponemos el número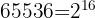 
Como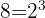 
, entonces:
Igualamos las potencias
2 
Trasformamos las raíces en potencias de exponente fraccionario e igualamos los exponentes
Resolvemos la ecuación resultante:
3 
Extraemos factor común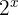 
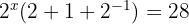
Aplicamos la ley de potencia negativa y resolvemos las operaciones y despejamos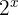
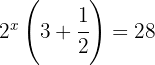
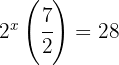
Reescribimos la ecuación con la misma base e igualamos los exponentes
Caso 2: La suma de los términos de una progresión geométrica
Si tenemos la suma de los 
términos de una progresión geométrica, aplicamos la fórmula:
Ejemplo
Aplicando la fórmula de la suma de los términos de una progresión geométrica:
Despejamos 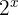y expresamos ambos miembros con la misma base
Caso 3: Cambio de variable
Cuando tenemos una ecuación más compleja podemos recurrir a un cambio de variable.
Ejemplos
1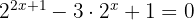 
En primer lugar aplicamos las propiedad del producto de potencias para quitar la suma del exponente.
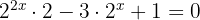
Aplicamos la propiedad de potencia de otra potencia
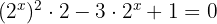
Realizamos el cambio de variable 
Factorizando la ecuación y resolviendo
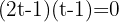
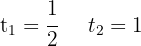
Deshacemos el cambio de variable
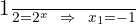
2 
Aplicamos las propiedades de las potencias del producto o el cociente, para quitar las sumas o restas de los exponentes
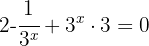
Hacemos el cambio de variable 
Multiplicamos ambos miembros por 
Factorizamos y resolvemos la ecuación
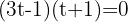
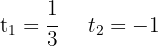
Deshacemos el cambio de variable
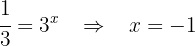
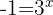
De la segunda ecuación no se obtiene solución
3 
Descomponemos en factores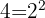 
y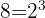
Realizamos el cambio de variable
Deshacemos el cambio de variable solo con la solución positiva.
Como no podemos igualar exponentes tomamos logaritmos en los dos miembros y en el primer miembro aplicamos la propiedad:
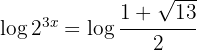
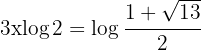
Despejamos la 
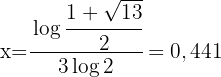
Para la otra solución de signo negativo no tendríamos solución porque al aplicar logaritmos en el segundo miembro nos encontraríamos con el logaritmo de un número negativo, que no existe.
Caso 4: No se pueden expresar ambos miembros con la misma base
Para despejar una incógnita que está en el exponente de una potencia, se toman logaritmos cuya base es la base de la potencia.
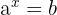
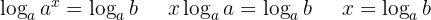
Ejemplo
1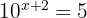 
Tomamos logaritmos en los dos miembros
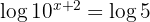
Aplicamos la propiedad del logaritmo de una potencia
Como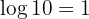 
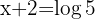
Despejamos
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayuda por favor con un logaritmo
Log3 (10-×) – log3 (3×-2) =2.
(√2+1)^X+(√2-1)^X=6
Puedes ayudarme?
Gracias
Hola muy buenos días me ayudaría con este ejercicio
(a²-1÷b)^n(a-1÷b)^-2n ÷(b²-1÷a²)-n(b+1÷a)^2n
3log(6-x)-log(72-x^3)=0
Log(2x-7)-log(x-1)=log5
saca el factor comun de la x y luego divide
Prof. : Log (35_X)= 3Log(5_x) siguiendo uno parecido de usted, llegue hasta aqui: 15X al cuadrado _ 75x _90=0 ayuda por favor.