Temas

Ecuación logarítmica
En las ecuaciones logarítmicas la incógnita aparece dentro del argumento de un logaritmo.
Antes de resolver ecuaciones logarítmicas debemos tener presentes las propiedades de los logaritmos.
Propiedades de los logaritmos
1 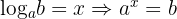
2 
3 
4 
5 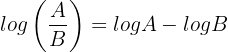
6 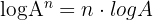
Además tenemos que comprobar las soluciones para verificar que no tenemos el logaritmo de un número negativo o de cero, esto es muy frecuente cuando tenemos una expresión de segundo grado en el argumento del logaritmo.
Ejemplos de resolución de ecuaciones logarítmicas
Resolver las siguientes ecuaciones logarítmicas
1
Para resolver esta ecuación basta con aplicar la propiedad  (Definición de logaritmo):
(Definición de logaritmo):


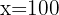
2 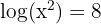
Podemos aplicar la propiedad  , despejar y posteriormente la propiedad
, despejar y posteriormente la propiedad  :
:
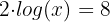
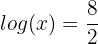
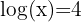
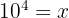

3
Aplicamos la propiedad 1 y luego despejamos la variable 
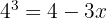

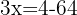
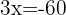
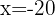
En el primer miembro aplicamos el logaritmo de un producto y en segundo la propiedad del logaritmo de una potencia.
 Usando las propiedades de los logaritmos podemos expresar como un solo logaritmo cada miembro de la ecuación. Para el primer miembro podemos emplear la propiedad
Usando las propiedades de los logaritmos podemos expresar como un solo logaritmo cada miembro de la ecuación. Para el primer miembro podemos emplear la propiedad  y en el segundo miembro la
y en el segundo miembro la  :
: 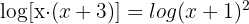
Una vez que ambos miembros están expresados en función de un sólo logaritmo, podemos igualar sus argumentos (Inyectividad de los logaritmos):
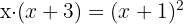
Resolvemos la ecuación resultante:
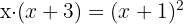
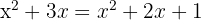
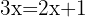

5 
El denominador del primer miembro multiplica al segundo miembro de la ecuación:
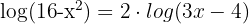
Aplicamos la propiedad  e igualamos los argumentos de los logaritmos:
e igualamos los argumentos de los logaritmos:

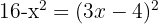
Resolvemos la ecuación:
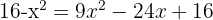

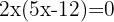

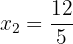
En este caso, debemos verificar si alguna de las soluciones nos indetermina algún logaritmo:
Usando  :
:
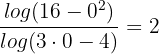
En el denominador obtendríamos:

lo cual es una indeterminación, ya que no es posible calcular el logaritmo de un número negativo. Por lo tanto, la solución de la ecuación sería 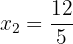 .
.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Ayuda por favor con un logaritmo
Log3 (10-×) – log3 (3×-2) =2.
(√2+1)^X+(√2-1)^X=6
Puedes ayudarme?
Gracias
Hola muy buenos días me ayudaría con este ejercicio
(a²-1÷b)^n(a-1÷b)^-2n ÷(b²-1÷a²)-n(b+1÷a)^2n
3log(6-x)-log(72-x^3)=0