
Binomios al cuadrado
1 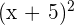
2 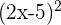
3 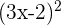
4 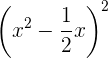
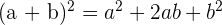
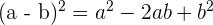
1 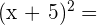
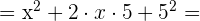

2 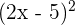
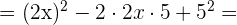

3

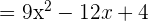
4 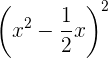


Binomios al cubo
1 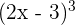
2 
3 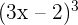
4 
Un binomio al cubo es igual al cubo del primero más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo.
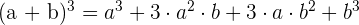
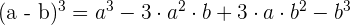
1 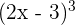
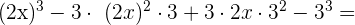
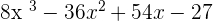
2 
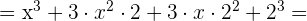
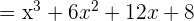
3 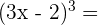
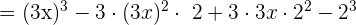
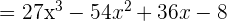
4 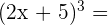
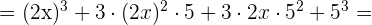
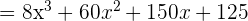
Productos de binomios
1 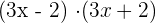
2 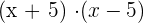
3 
4 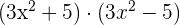
1
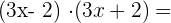
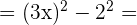

2 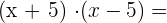

3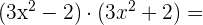
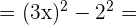
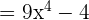
4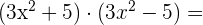

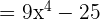
Más productos notables
1 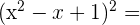
2 
3 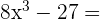
4 
Un trinomio al cuadrado es igual al cuadrado del primero, más el cuadrado del segundo, más el cuadrado del tercero, más el doble producto del primero por el segundo, más el doble producto del primero por el tercero, más el doble producto del segundo por el tercero.
El desarrollo de una suma de cubos es:
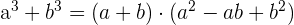
1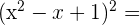
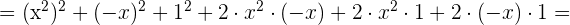
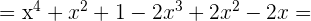
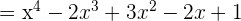
2 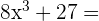
Entonces:
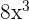 es el cubo de
es el cubo de  y
y  es el cubo de
es el cubo de 
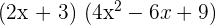
3 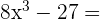
El desarrollo de una diferencia de cubos es:

Entonces:
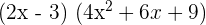
4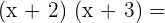
Este producto se puede realizar multiplicando cada uno de los sumandos del primer factor por cada uno de los sumandos del segundo factor.

También se puede realizar como el producto de dos binomios que tienen un término común:
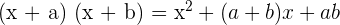
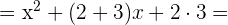
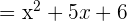













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
-12X-8-3X+10=2X-9+8Y
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Mesecito ayuda de matemáticas
Puedes obtenerla en https://www.superprof.es/ 🙂
Halla el cociente y el residuo de las divisiones siguientes
(.^3-3.^2+2.-2)\(.+1)
Alguien me ayuda en este problema de polinomios 1. P(x) = 7
2. Q(x) = 4x
2 − 1
3. R(x) = 2x
4 + 5
4. S(x) = x
5 + 2x
2 − 7
5. T(x) = 4x
6 + 2x
3 − 1
6. U(x) = 5x
8