Temas
- Decide si las siguientes expresiones algebraicas son polinomios o no
- Escribe en lenguaje matemático
- Dados los polinomios, P,Q,R,U y expresiones algebraicas S,T:
- Dados los polinomios, P,Q,R:
- Realiza las siguientes multiplicaciones
- Realiza las siguientes divisiones
- Divide utilizando la regla de Ruffini
- Sin efectuar las divisiones, halla el resto de las siguientes operaciones
- Indica cuáles de estas divisiones son exactas
- Comprueba que los siguientes polinomios tienen como factores los que se indican
- Calcula los valores que se indican
- Calcula los coeficientes que se te indican
- Calcula el valor de k
- Calcula el valor de m
- Encuentra el polinomio que cumpla con lo siguiente
- Calcula el valor de a
Ejercicios resueltos de grado y término independiente de polinomio, polinomios ordenados, sumas y restas de polinomios, multiplicación de polinomios, división de polinomios, división por Ruffini, teorema del resto, resto de un polinomio, y teorema del factor.

Decide si las siguientes expresiones algebraicas son polinomios o no
Decide si las siguientes expresiones algebraicas son polinomios o no.
En caso afirmativo, señala cuál es su grado y término independiente.
1 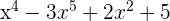
2 
3 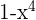
4 
5 
6 
7 
1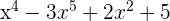
Grado:  , término independiente:
, término independiente:  .
.
2 
No es un polinomio, porque la parte literal del primer monomio está dentro de una raíz.
3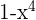
Grado:  , término independiente:
, término independiente:  .
.
4 
No es un polinomio, porque el exponente  del primer monomio no es un número natural.
del primer monomio no es un número natural.
5 
Grado:  , término independiente:
, término independiente: .
.
6 
No es un polinomio, porque el exponente del segundo monomio no es un número natural.
7 
Grado:  , término independiente:
, término independiente:  .
.
Escribe en lenguaje matemático
1 Un polinomio ordenado sin término independiente.
2 Un polinomio no ordenado y completo.
3 Un polinomio completo sin término independiente.
4 Un polinomio de grado  , completo y con coeficientes impares.
, completo y con coeficientes impares.
Escribe:
1 Un polinomio ordenado sin término independiente.
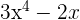
2 Un polinomio no ordenado y completo.
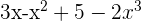
3 Un polinomio completo sin término independiente.
Imposible
4 Un polinomio de grado  , completo y con coeficientes impares.
, completo y con coeficientes impares.

Dados los polinomios, P,Q,R,U y expresiones algebraicas S,T:
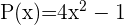
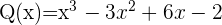
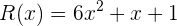



Calcular:
1 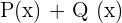
2 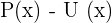
3 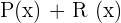
4 
5 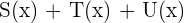
6 
Dados los polinomios y expresiones algebraicas:
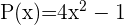
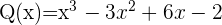
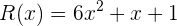



Calcular:
1 
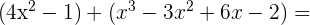
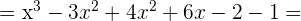
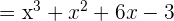
2
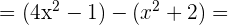


3 
= 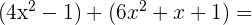
= 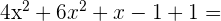
= 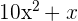
4 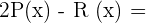



5 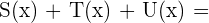
= 
= 
= 
6 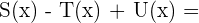
= 
= 
= 
Dados los polinomios, P,Q,R:
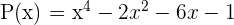


Calcular:
1 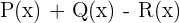
2 
3 
Dados los polinomios:
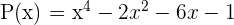

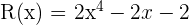
Calcular:
1 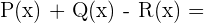

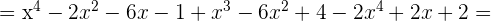


2 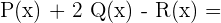


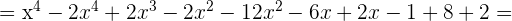
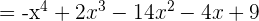
3 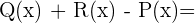

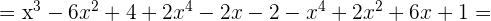
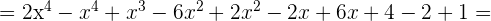
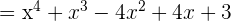
Realiza las siguientes multiplicaciones
1 
2 
3 
Realiza las siguientes multiplicaciones
1 
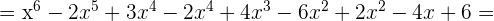
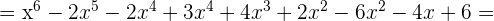
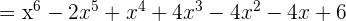
2 
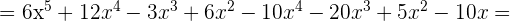
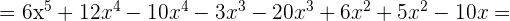

3 
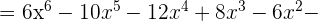
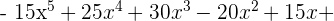
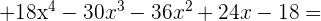

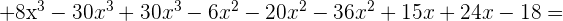
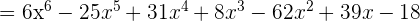
Realiza las siguientes divisiones
1 
2 
3 Dados los polinomios:
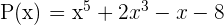

Resolver

Realiza las siguientes divisiones
1 

2 

3 Dados los polinomios:
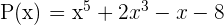

Resolver
 :
:

Divide utilizando la regla de Ruffini
1 
2 
3 
Divide por Ruffini:
1 

![]()
2 

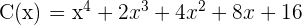
3 

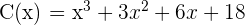
Sin efectuar las divisiones, halla el resto de las siguientes operaciones
1 
2 
3 
Sin efectuar las divisiones, halla el resto de las siguientes Operaciones:
Para hallar el resto emplearemos el teorema del resto que nos dice que el resto de la división de un polinomio  , entre un polinomio de la forma
, entre un polinomio de la forma  es el valor numérico de dicho polinomio para el valor:
es el valor numérico de dicho polinomio para el valor: 
1 
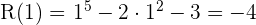
2 
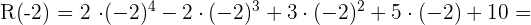
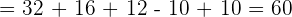
3 

Indica cuáles de estas divisiones son exactas
Indica cuáles de estas divisiones son exactas:
1 
2 
3 
4 
Indica cuáles de estas divisiones son exactas:
1Aplicamos el teorema del resto, si el resto es cero la división será exacta.


No es exacta.
2 
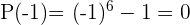
Exacta.
3 
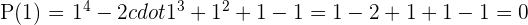
Exacta.
4 
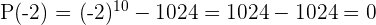
Exacta.
Comprueba que los siguientes polinomios tienen como factores los que se indican
1 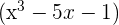 tiene por factor
tiene por factor 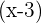
2  tiene por factor
tiene por factor 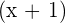
3 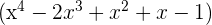 tiene por factor
tiene por factor 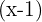
4  tiene por factor
tiene por factor 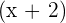
Comprueba que los siguientes polinomios tienen como factores los que se indican:
1 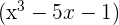 tiene por factor
tiene por factor 
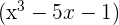 es divisible por
es divisible por  si y sólo si
si y sólo si  .
.

 no es un factor.
no es un factor.
2 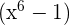 tiene por factor
tiene por factor 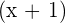
 es divisible por
es divisible por 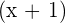 si y sólo si
si y sólo si  .
.
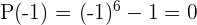
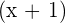 es un factor.
es un factor.
3 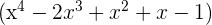 tiene por factor
tiene por factor 
 .
.

 es un factor.
es un factor.
4 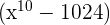 tiene por factor
tiene por factor 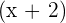
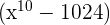 es divisible por
es divisible por 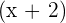 si y sólo si
si y sólo si  .
.
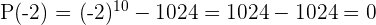
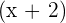 es un factor.
es un factor.
Calcula los valores que se indican
Hallar  y
y  para que el polinomio
para que el polinomio 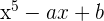 sea divisible por
sea divisible por 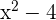 .
.
Hallar  y
y  para que el polinomio
para que el polinomio 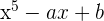 sea divisible por
sea divisible por 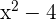 .
.
Descomponemos en factores la diferencia de cuadrados

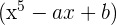 es divisible por
es divisible por  si y sólo si
si y sólo si  y
y 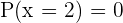
Aplicamos el teorema del resto sabiendo que el resto es cero

Operamos


Aplicamos el teorema del resto sabiendo que el resto es cero

Operamos
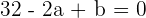

Hemos obtenido dos ecuaciones con dos incógnitas. Resolveremos el sistema por reducción

![]()
Calcula los coeficientes que se te indican
Determina los coeficientes de  y
y  para que el polinomio
para que el polinomio 
sea divisible por 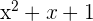 .
.
Determina los coeficientes de  y
y  para que el polinomio
para que el polinomio 
sea divisible por 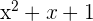 .
.
Efectuamos la división

Para que sea divisible la división tiene que ser exacta, es decir,
el resto tiene que ser cero.
Para que el resto sea cero el coeficiente de la  y el coeficiente
y el coeficiente
del término independiente han de ser cero
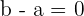
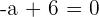


Calcula el valor de k
Encontrar el valor de  para que al dividir
para que al dividir 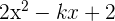 por
por 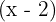 dé como resto
dé como resto  .
.
Encontrar el valor de  para que al dividir
para que al dividir 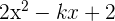 por
por 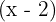 dé como resto
dé como resto  .
.
Aplicamos el teorema del resto y sabemos que el resto es 

Operamos
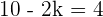
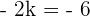

Calcula el valor de m
Determinar el valor de m para que 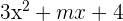 admita
admita  como una de sus raíces.
como una de sus raíces.
Determinar el valor de  para que
para que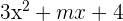 admita
admita  como una de sus raíces.
como una de sus raíces.
Si  es una raíz del polinomio, entonces el valor numérico del polinomio para ese valor ha de ser cero
es una raíz del polinomio, entonces el valor numérico del polinomio para ese valor ha de ser cero

Operamos


Encuentra el polinomio que cumpla con lo siguiente
Hallar un polinomio de cuarto grado que sea divisible por 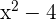
y se anule para  y
y  .
.
Hallar un polinomio de cuarto grado que sea divisible por 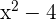
y se anule para 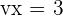 y
y  .
.
Si se anula para  y
y  , entonces
, entonces  y
y 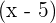 son factores
son factores
del polinomio buscado
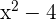 es otro factor, ya que el polinomio es divisble por
es otro factor, ya que el polinomio es divisble por 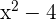
Multiplicamos los factores:

En primer lugar multiplicamos los dos primeros
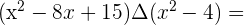
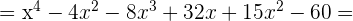
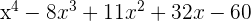
Calcula el valor de a
Calcular el valor de a para que el polinomio 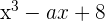 tenga la raíz
tenga la raíz  ,
,
y calcular las otras raíces.
Calcular el valor de a para que el polinomio 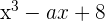 tenga la raíz
tenga la raíz  ,
,
y calcular las otras raíces.
Calculamos el valor de  sabiendo que el valor numérico del polinomio para
sabiendo que el valor numérico del polinomio para
 tiene que ser cero
tiene que ser cero


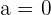
Factorizamos dividendo por Ruffini


Igualamos el segundo factor a cero y resolvemos la ecuación de segundo grado
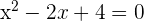
![]()
No tiene más raíces reales.
Si necesitas más ayuda, no dudes en contactar con Superprof y te ayudamos con el mejor curso de matematicas. En la plataforma podrás encontrar tanto un profesor de matematicas online como uno presencial.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
-12X-8-3X+10=2X-9+8Y
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Mesecito ayuda de matemáticas
Puedes obtenerla en https://www.superprof.es/ 🙂
Halla el cociente y el residuo de las divisiones siguientes
(.^3-3.^2+2.-2)\(.+1)
Alguien me ayuda en este problema de polinomios 1. P(x) = 7
2. Q(x) = 4x
2 − 1
3. R(x) = 2x
4 + 5
4. S(x) = x
5 + 2x
2 − 7
5. T(x) = 4x
6 + 2x
3 − 1
6. U(x) = 5x
8