Temas
Si prefieres aprender desde casa, ¿por qué no buscas un profesor matematicas online? ¡La primera clase es gratis!
Los ejercicios que a continuación resolveremos, son ejemplos de:
- Factorización de un binomio
- Factorización de un trinomio cuadrado perfecto
- Factorización de un trinomio cuadrado perfecto
- Factorización de un trinomio de segundo grado
- Factorización de un polinomio de cuarto grado
- Factorización del polinomio de tercer grado incompleto
- Orden de la ecuación para facilitar la factorización

Ejercicios de factorización para obtener las raíces de los polinomios
1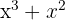
1Para factorizar 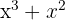 , notamos que
, notamos que  es factor común de ambos términos
es factor común de ambos términos
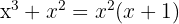
2Sabemos que las raíces, es el valor que toma  tal que la ecuación es igual a cero, entonces, dado
tal que la ecuación es igual a cero, entonces, dado 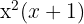 , existen 2 casos: cuando
, existen 2 casos: cuando  y cuando
y cuando 
Así, las raíces son  y
y 
2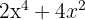
1Para factorizar 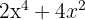 , notamos que
, notamos que 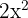 es factor común de cada uno de los términos
es factor común de cada uno de los términos
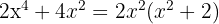
2En este caso solo existe la raiz  , ya que el polinomio
, ya que el polinomio  no tiene raíces, esto es, no existe un número real
no tiene raíces, esto es, no existe un número real  tal que
tal que 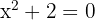
3
1Aplicamos diferencia de cuadrados
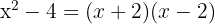
2Igualando cada factor a cero se obtienen las raíces
 y
y 
4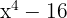
1Aplicamos diferencia de cuadrados

2Aplicamos nuevamente diferencia de cuadrados al segundo factor

3Igualando cada factor a cero se obtienen las raíces
 y
y 
Recuerda que el factor  no posee raíces reales
no posee raíces reales
5 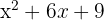
1Nos encontramos con un trinomio cuadrado perfecto, el cual puede escribirse como un binomio al cuadrado, para lo cual tenemos que preguntarnos
¿Qué número elevado al cuadrado da  ?, ¿qué número elevado al cuadrado da
?, ¿qué número elevado al cuadrado da 
y comprobar que el doble del producto de los dos resultados es igual a 
2Lo anterior se satisface para  y
y  , por lo que la factorización se expresa como sigue
, por lo que la factorización se expresa como sigue

3Igualando cada factor a cero se obtienen las raíces
 y se dice que es una raíz doble
y se dice que es una raíz doble
6
1En este caso usaremos la formula general para ecuaciones de segundo grado para lo cual debemos igualar la ecuación a cero, es decir  . Encontramos los valores de
. Encontramos los valores de  (raices de la ecuacion) utilizando la formula general
(raices de la ecuacion) utilizando la formula general
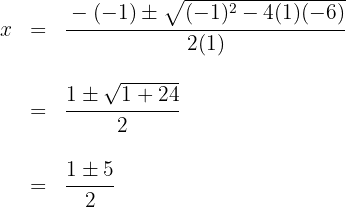
Al resolver se obtienen las raíces 
2En este caso los factores de la ecuación dada son
 .
.
7
1Igualamos el polinomio a cero y hacemos un cambio de variable 
Sustituyendo nuestra nueva variable tenemos 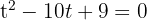
2Resolvemos la ecuación de segundo grado
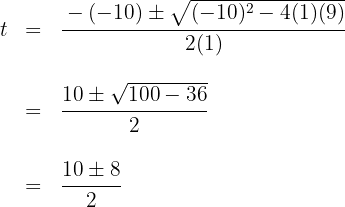
Al resolver se obtienen las raíces 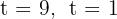
3Ahora, en nuestro cambio de variable teníamos que  ; deshacemos el cambio de variable y obtenemos las raíces
; deshacemos el cambio de variable y obtenemos las raíces

4En este caso los factores de la ecuación dada son
 .
.
8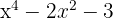
1Igualamos el polinomio a cero y hacemos un cambio de variable 
Sustituyendo nuestra nueva variable tenemos 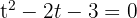
2Resolvemos la ecuación de segundo grado

Al resolver se obtienen las raíces 
3Ahora, en nuestro cambio de variable teníamos que  ; deshacemos el cambio de variable y obtenemos las raíces
; deshacemos el cambio de variable y obtenemos las raíces
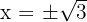 ; pero
; pero 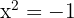 no posee soluciones reales
no posee soluciones reales
4En este caso los factores de la ecuación dada son
 .
.
9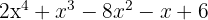
1 Tomamos los divisores del término independiente, estos son,  .
.
2 Aplicando el teorema del resto sabremos para que valores la división es exacta.

3 Dividimos por Ruffini.
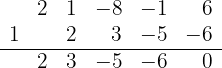
Como la división es exacta,  es una raíz y el polinomio se expresa
es una raíz y el polinomio se expresa

4 Continuamos realizando las mismas operaciones al segundo factor. Volvemos a probar por  porque el primer factor podría estar elevado al cuadrado.
porque el primer factor podría estar elevado al cuadrado.

Luego  no es raíz del segundo factor. Probamos con
no es raíz del segundo factor. Probamos con 
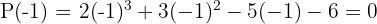
5 Dividimos por Ruffini.
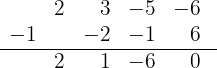
Como la división es exacta,  es una raíz y el polinomio se expresa
es una raíz y el polinomio se expresa
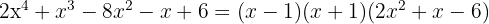
6 El tercer factor lo podemos encontrar aplicando la ecuación de segundo grado o tal como venimos haciéndolo, aunque tiene el inconveniente de que sólo podemos encontrar raíces enteras.
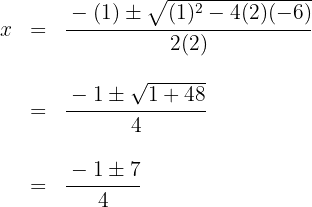
Las raíces son 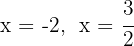 y el polinomio se expresa
y el polinomio se expresa
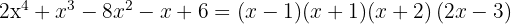
10
1 Tomamos los divisores del término independiente, estos son, 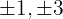 .
.
2 Aplicando el teorema del resto sabremos para que valores la división es exacta.
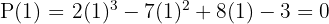
3 Dividimos por Ruffini.
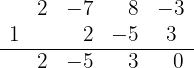
Como la división es exacta,  es una raíz y el polinomio se expresa
es una raíz y el polinomio se expresa

4 Continuamos realizando las mismas operaciones al segundo factor. Volvemos a probar por  porque el primer factor podría estar elevado al cuadrado.
porque el primer factor podría estar elevado al cuadrado.

5 Dividimos por Ruffini.

Como la división es exacta,  es una raíz doble y el polinomio se expresa
es una raíz doble y el polinomio se expresa
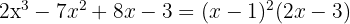
11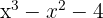
1 Tomamos los divisores del término independiente, estos son, 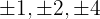 .
.
2 Aplicando el teorema del resto sabremos para que valores la división es exacta.
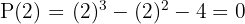
3 Dividimos por Ruffini.
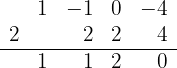
Como la división es exacta,  es una raíz y el polinomio se expresa
es una raíz y el polinomio se expresa
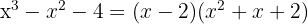
4 El segundo factor lo podemos encontrar aplicando la ecuación de segundo grado o tal como venimos haciéndolo, aunque tiene el inconveniente de que sólo podemos encontrar raíces enteras.
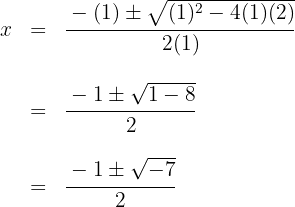
Como el discriminante es negativo, el polinomio no posee raíces reales. Así, la única raíz es  y el polinomio se expresa
y el polinomio se expresa
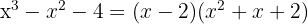
12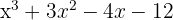
1 Tomamos los divisores del término independiente, estos son, 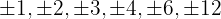 .
.
2 Aplicando el teorema del resto sabremos para que valores la división es exacta.

3 Dividimos por Ruffini.
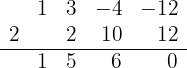
Como la división es exacta,  es una raíz y el polinomio se expresa
es una raíz y el polinomio se expresa
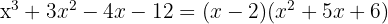
4 El segundo factor lo podemos encontrar aplicando la ecuación de segundo grado o tal como venimos haciéndolo, aunque tiene el inconveniente de que sólo podemos encontrar raíces enteras.
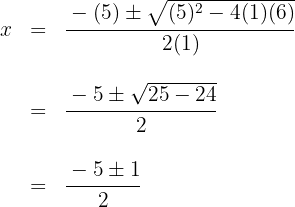
Las raíces del segundo factor son 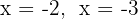 y el polinomio se expresa
y el polinomio se expresa
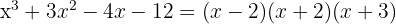
13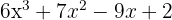
1 Tomamos los divisores del término independiente, estos son,  .
.
2 Aplicando el teorema del resto sabremos para que valores la división es exacta.
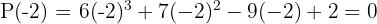
3 Dividimos por Ruffini.

Como la división es exacta,  es una raíz y el polinomio se expresa
es una raíz y el polinomio se expresa

4 El segundo factor lo podemos encontrar aplicando la ecuación de segundo grado o tal como venimos haciéndolo, aunque tiene el inconveniente de que sólo podemos encontrar raíces enteras.
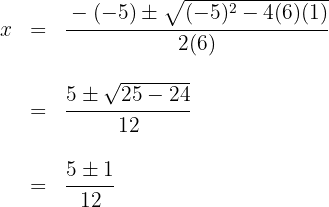
Las raíces del segundo factor son  y el polinomio se expresa
y el polinomio se expresa

Si buscas un profesor de mates, ¿has probado los de Superprof? Tenemos para todos los gustos y niveles y, además, ¡la primera clase es gratis!
Ejercicios de factorizacíon de polinomios
1 
2 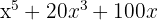
3 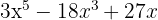
4 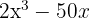
5 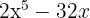
6 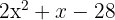
1
Sacamos factor común 
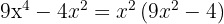
Escribimos la diferencia de cuadrados como una suma por diferencia
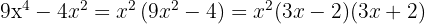
2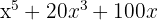
Extraemos factor común 

Tenemos un trinomio cuadrado perfecto que lo podemos expresar como un binomio al cuadrado
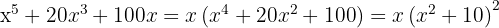
3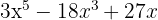
Extraemos factor común 
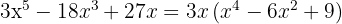
Tenemos un trinomio cuadrado perfecto que lo podemos expresar como un binomio al cuadrado

Escribimos la diferencia de cuadrados como una suma por diferencia
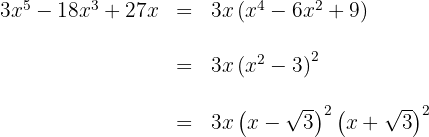
4 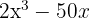
Sacamos factor común 
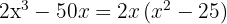
Escribimos la diferencia de cuadrados como una suma por diferencia

5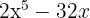
Extraemos factor común 

Escribimos la diferencia de cuadrados como una suma por diferencia
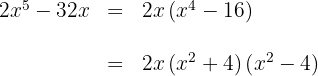
El segundo factor es un polinomio irreducible o primo
El tercer factor es una diferencia de cuadrados que factorizamos como una suma por diferencia
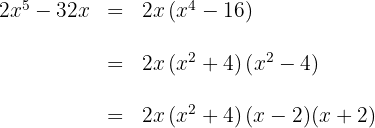
6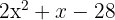
El trinomio de segundo grado lo igualamos a cero y resolvemos la ecuación

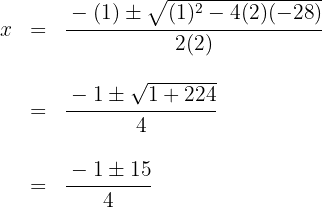
Las raíces son 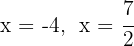 y el polinomio se expresa
y el polinomio se expresa
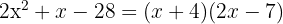
Ejercicios de descomposición en factores de polinomios
Si vives en la capital, ¿por qué no pruebas nuestras clases particulares matematicas Madrid? ¡Tenemos profes para todos los gustos y niveles!
1
2
3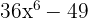
4
5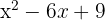
6
7
8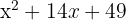
9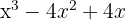
10
11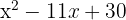
12
13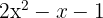
1
En este ejercicio podemos hacer una doble extracción de factor común. En los dos primeros sumandos extraemos  y en los dos últimos extraemos
y en los dos últimos extraemos 

Sacamos factor común 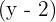

2
es una diferencia de cuadrados
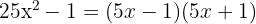
3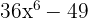
La diferencia de cuadrados es igual a suma por diferencia
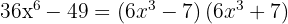
4
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado
El cuadrado de  es
es  , el cuadrado de
, el cuadrado de  es
es  y el doble del primero
y el doble del primero  por el segundo
por el segundo  es
es 

5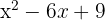
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado
El cuadrado de  es
es  , el cuadrado de
, el cuadrado de  es
es  y el doble del primero
y el doble del primero  por el segundo
por el segundo  es
es 
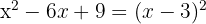
6
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado
El cuadrado de  es
es  , el cuadrado de
, el cuadrado de  es
es  y el doble del primero
y el doble del primero  por el segundo
por el segundo  es
es 
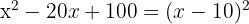
7
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado
El cuadrado de  es
es  , el cuadrado de
, el cuadrado de  es
es  y el doble del primero
y el doble del primero  por el segundo
por el segundo  es
es 

8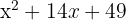
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado
El cuadrado de  es
es  , el cuadrado de
, el cuadrado de  es
es  y el doble del primero
y el doble del primero  por el segundo
por el segundo  es
es 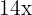
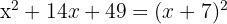
9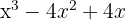
Sacamos factor común

Tenemos otro trinomio cuadrado perfecto
El cuadrado de  es
es  , el cuadrado de
, el cuadrado de  es
es  y el doble del primero
y el doble del primero  por el segundo
por el segundo  es
es 
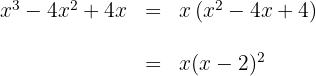
10
Sacamos factor común
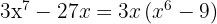
La diferencia de cuadrados la transformamos en una suma por diferencia

Aplicamos suma y diferencia de cubos

11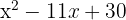
Igualamos el polinomio a cero
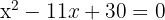
Resolvemos la ecuación de segundo grado
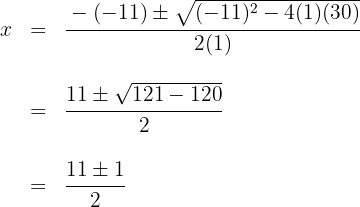
Las raíces son 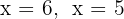 y el polinomio se expresa
y el polinomio se expresa

12
Resolvemos la ecuación de segundo grado

Las raíces son 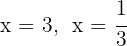 y el polinomio se expresa
y el polinomio se expresa
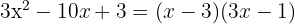
13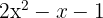
Resolvemos la ecuación de segundo grado
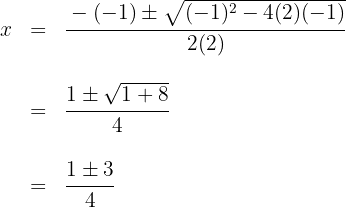
Las raíces son 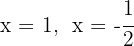 y el polinomio se expresa
y el polinomio se expresa














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
-12X-8-3X+10=2X-9+8Y
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Mesecito ayuda de matemáticas
Puedes obtenerla en https://www.superprof.es/ 🙂
Halla el cociente y el residuo de las divisiones siguientes
(.^3-3.^2+2.-2)\(.+1)
Alguien me ayuda en este problema de polinomios 1. P(x) = 7
2. Q(x) = 4x
2 − 1
3. R(x) = 2x
4 + 5
4. S(x) = x
5 + 2x
2 − 7
5. T(x) = 4x
6 + 2x
3 − 1
6. U(x) = 5x
8