Paolo Ruffini (1765, 1822) fue un matemático italiano, que estableción un método más breve para hacer la división de polinomios, cuando el divisor es un binomio de la forma x — a.

Regla de Ruffini
Para explicar los pasos a aplicar en la regla de Ruffini vamos a tomar dos ejemplos:
Primer ejemplo de la regla de Ruffini
Dividir: 
1 Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.
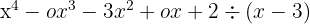
2Colocamos los coeficientes del dividendo en una línea.

3Abajo a la izquierda colocamos el opuesto del término independiente del divisor: 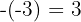 .
.


4Trazamos una raya y bajamos el primer coeficiente  .
.
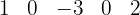
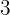

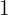
5Multiplicamos ese coeficiente  por el divisor
por el divisor 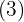 y lo colocamos debajo del siguiente término
y lo colocamos debajo del siguiente término 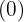 .
.
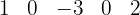


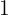
6Sumamos los dos coeficientes 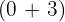 .
.
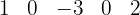



7Repetimos el proceso anterior 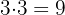 et
et 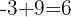 ).
).
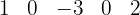



Volvemos a repetir el proceso 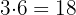 et
et 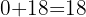 (.
(.
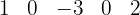


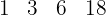
Volvemos a repetir  et
et 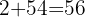 .
.
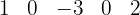



8El último número obtenido, 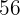 , es el resto.
, es el resto.
9El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido.
Cociente: 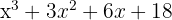
Resto: 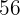
Segundo ejemplo de la regla de Ruffini
Dividir por la regla de Ruffini: 
1 Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.
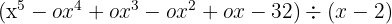
2Colocamos los coeficientes del dividendo en una línea.
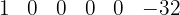
3Abajo a la izquierda colocamos el opuesto del término independiente del divisor: 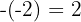 .
.


4Trazamos una raya y bajamos el primer coeficiente  .
.



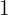
5Multiplicamos ese coeficiente  por el divisor
por el divisor  y lo colocamos debajo del siguiente término
y lo colocamos debajo del siguiente término 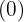 .
.



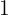
6Sumamos los dos coeficientes  .
.




7 Repetimos los pasos  y
y  hasta el final.
hasta el final.

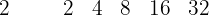

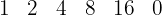
8 El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido.
Cociente: 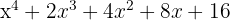
Resto: 













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
El valor númerico de la expresión 7(x²-2x+5)/3 , cuando x =-2
-12X-8-3X+10=2X-9+8Y
(2x-1)(3x-5)-6x(2÷3x-1÷2)
10x + 2x
Mesecito ayuda de matemáticas
Puedes obtenerla en https://www.superprof.es/ 🙂
Halla el cociente y el residuo de las divisiones siguientes
(.^3-3.^2+2.-2)\(.+1)
Alguien me ayuda en este problema de polinomios 1. P(x) = 7
2. Q(x) = 4x
2 − 1
3. R(x) = 2x
4 + 5
4. S(x) = x
5 + 2x
2 − 7
5. T(x) = 4x
6 + 2x
3 − 1
6. U(x) = 5x
8