Capítulos
Un polinomio 
es divisible por un polinomio de la forma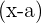 
si y sólo si 
es un cero o raíz de .
Raíces de un polinomio
Las raíces o ceros de un polinomio son los valores que anulan el polinomio, por tanto su valor númerico es cero, esto es, es una raíz de si 
.
Ejemplo:
Comprobar que 2 y 3 son las raíces del polinomio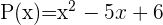 
.
1 Evaluamos 2 y 3 en y verificamos si el resultado es cero.
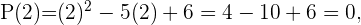
2 Concluimos que 2 y 3 son raíces del polinomio .
Propiedades de las raíces y factores de un polinomio
1Los ceros o raíces enteras de un polinomio son divisores del término independiente del polinomio.
Ejemplo:
Si tenemos [Latex]{P(x) = x^2-6x + 8}[/latex], las posibles raíces son divisores de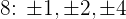 
y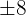 
.
Evaluamos las posibles raíces en el polinomio y notamos que 2 y 4 son los únicos valores con los que se obtiene cero
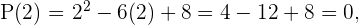
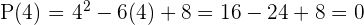
Concluimos que 2 y 4 son raíces del polinomio 
.
2A cada raíz del tipo 
, le corresponde un binomio del tipo .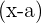
Ejemplo:
Para 
, le corresponde el binomio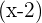 
.
Para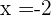 
, le corresponde el binomio 
.
3Podemos expresar un polinomio en factores al escribirlo como producto de todos los binomios del tipo 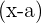, que se correspondan a las raíces, , que se obtengan.
Ejemplo
4La suma de los exponentes de los binomios ha de ser igual al grado del polinomio.
Ejemplos:
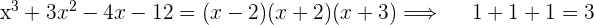
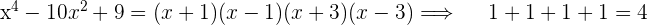
5Todo polinomio que no tenga término independiente admite como raíz 
, o lo que es lo mismo, admite como factor 
.
Ejemplo
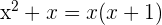
Raíces: y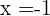 
6Un polinomio se llama irreducible (primo) cuando no puede descomponerse en factores.
Ejemplo:
Las posibles raíces son los divisores del término independiente son 
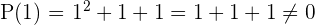
Cálculo de las raíces y factores de un polinomio
Partimos de los divisores del término independiente, con estos valores aplicamos el teorema del resto o residuo y sabremos para que valores la división es exacta.
Ejemplo:
Encontrar las raíces del polinomio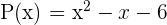 
.
1 Buscamos los divisores del término independiente, estos son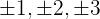 
.
2 Evaluamos los divisores en el polinomio
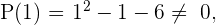
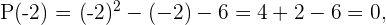
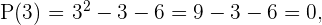
Como el polinomio es de segundo grado tendrá como máximo dos raíces
3 Las raíces son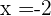 
y 
.
4 La factorización del polinomio es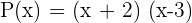 
Ejemplo:
Encontrar las raíces del polinomio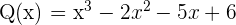 
1 Buscamos los divisores del término independiente, estos son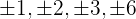 
.
2 Evaluamos los divisores en el polinomio
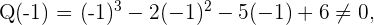
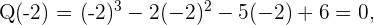
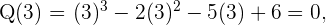
Como el polinomio es de tercer grado tendrá como máximo tres raíces
3 Las raíces son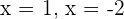 
y .
4 La factorización del polinomio es 
Ejemplo:
Encontrar las raíces del polinomio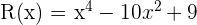 
1 Buscamos los divisores del término independiente, estos son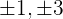 
.
2 Evaluamos los divisores en el polinomio
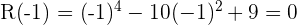
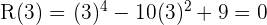
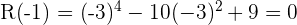
Como el polinomio es de cuarto grado tendrá como máximo cuatro raíces
3 Las raíces son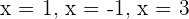 
y 
.
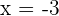4 La factorización del polinomio es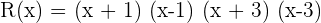 
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Escribo y elijo bien las respuestas y me aparece el setenta porciento, no entiendo porque si todas me quedan bien.
Hola te agradecemos por visitar nuestra pagina, en cuanto a lo que pasa con los resultados del cuestionario, se supone que la pagina te da las respuestas de los ejercicios y allí puedes ver cual ejercicio tiene el error, podrías por favor indicárnoslo para rectificarlo.
– 2 no es raíz del último polunomio
Hola gracias por tus observaciones, podrías hacernos el favor de mencionar el número del ejercicio para poder rectificarlo, seria de gran ayuda.
(14m³×+21m²)÷(-7)
Hola, una disculpa por el error ya se corrigió y gracias por la observación.
Hola cómo resuelvo esta suma algebraicas
7+8+4 =
_. _. _
7 5. 7