Chapters

Probability

| Bank Note | Amount |
| 50 pounds | 1 |
| 20 pounds | 1 |
| 5 pounds | 3 |
| Total Amount | 5 |
The probability of getting a 50 pound note is 1 divided by the total possible outcomes, 4, giving us 0.25 or 25%
Random Variable and Sample Space
To understand more complex notions of probability, it is necessary to understand the notation that is often used in probability theory. The table below summarizes some of the most important elements.
| Notation | Description | Example | |
| Random Variable | A | A variable whose outcomes are unknown | A coin toss |
| Probability | P() | The likelihood of something occurring | P(A) |
| Sample Space | S={} | All possible outcomes of a random variable | |
 | AND | The probability of event A AND B occurring | P(A  B) B) |
 | OR | The probability of event A OR B occurring | P(A  B) B) |
Independent Events
Two events are independent when the probability of the first event does not affect the probability of the second. This shouldn’t be confused with mutually exclusive events, which are events that cannot physically happen at the same time.
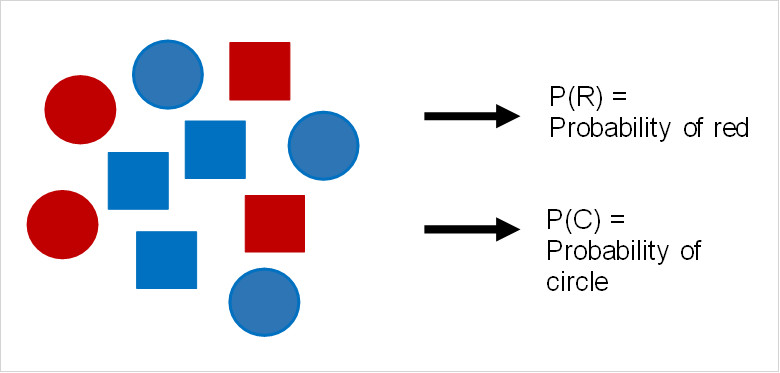
Let’s look at an example in the image above. Event A, selecting a red circle, is mutually exclusive from event B, selecting a blue circle. This is because it is not possible to select a red and blue circle at the same time.
If we pick a circle, but it back with the rest, then pick again, these two events are also independent. This is because picking a red circle, with probability 0.5, does not change in the next round because we’ve put the red circle back in and therefore have the same amount of circles as before.
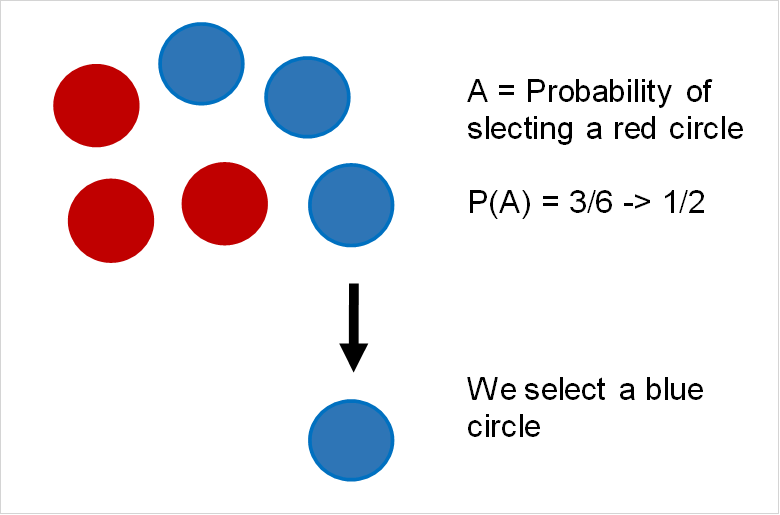

Dependent Events
Dependent events, on the other hand, are event whose probability is affected by the outcome of another event. Let’s take the example from before but this time we do not replace the circle we pick from the group.

While the two events A and B are still mutually exclusive, they are now dependent events. If in the first pick we select a red circle, that leaves us with only 5 circles: 2 red and 3 blue. The probability of picking a red circle for a second time is now only 2/5.

On the other hand, if you pick a blue circle the first time, that still leaves us with 5 circles, only now it would be: 3 red, 2 blue. The probability of picking a red circle for the second time would now be 3/5. In fact, whenever you’re picking without replacing, the events you’re studying will be dependent.
| Definition | Events | Example | |
| With Replacement | When you’re selecting something and then putting it back | Independent | Selecting cards out of a deck with replacement |
| Without Replacement | When you’re selecting something and then not putting it back | Dependent | Selecting cards out of a deck without replacement |
Conditional Probability
Card selections are a classic example of events that have conditional probability. If something is conditional, it means that it is dependent on something else happening. For example, the probability that you will bring an umbrella with you is conditional on, or dependent on, the probability that it will rain outside.

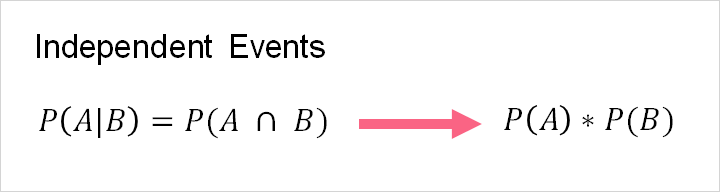
The formula above gives us the conditional probability of event A and B. The table below explains each element in the formula.
| Description | Example | |
| P(A|B) | The probability that event A will occur given that event B has already happened | The probability of selecting a king given that a spade has already been selected |
P(A  B) B) | The probability of A and B occurring | The probability of selecting a king and spade |
| P(B) | The probability of B | The probability of selecting a spade |
In order to calculate the probabilities, you should know that a deck of cards has:
- 4 kings
- 13 spades
| Probability | |
P(K  S) S) | 1/52 = 0.019 |
| P(S) | 13/52 = 0.25 |
| P(K|S) | 0.077 |
Bayes’ Theorem
Notice that the formula for conditional probability only applies to dependent events that are not mutually exclusive. If two events are independent, then the probability that A occurs is not affected by the fact that event B has occurred. On top of that, if two events are mutually exclusive, there is no way for event A and B to occur together, which gives us a conditional probability of 0.
| Mutually Exclusive | Not Mutually Exclusive | |
| Independent | P(A|B) = 0 P(B|A) = 0 | P(A|B) = P(A) P(B|A) = P(B) |
| Dependent | P(A|B) = 0 P(B|A) = 0 | P(A|B) =  P(B|A) = |
Another way of finding the conditional probability of events is with Bayes’ Theorem, which gives us the conditional probability of event A given B when we know the probability of event B given A.

Let’s try our King and Spade example with this formula, given that the probability of picking a Spade given a King has been picked is 0.25.
| Probability | |
| P(K) | 1/52 = 0.077 |
| P(S|K) | 0.25 |
| P(S) | 13/52 = 0.25 |
| P(K|S) | 0.077 |
Problem 1
Find the conditional probability of P(A|B) given the following information. Please keep in mind this is fictitious data.
| Description | Probability | |
| A | Fatal illnesses are quite rare | 0.005 = 0.5% |
| B | Coughs are very common, resulting from a number of illnesses | 0.3 = 30% |
| B|A | Coughs that occur due to fatal illnesses are also quite rare | 0.001 = 1% |
Solution 1
We can calculate P(A|B), or the probability of having a fatal illness given that we have a cough using Bayes’ formula.
| Description | Probability | |
| A | Fatal illnesses are quite rare | 0.005 = 0.5% |
| B | Coughs are very common, resulting from a number of illnesses | 0.3 = 30% |
| B|A | Coughs that occur due to fatal illnesses are also quite rare | 0.001 = 1% |
| A|B | A fatal illness given that we have a cough |  = =
|











 = 0.002%
= 0.002%


Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian
I’m a junior high school,500 students were randomly selected.240 liked ice cream,200 liked milk tea and 180 liked both ice cream and milktea
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
Where is the answer??
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
ere is a 60% chance that a final years student would throw a party before leaving school ,taken over 50 student from a total of 150 .calculate for the mean and the variance
There are 4 white balls and 30 blue balls in the basket. If you draw 7 balls from the basket without replacement, what is the probability that exactly 4 of the balls are white?