Chapters

Random Variable

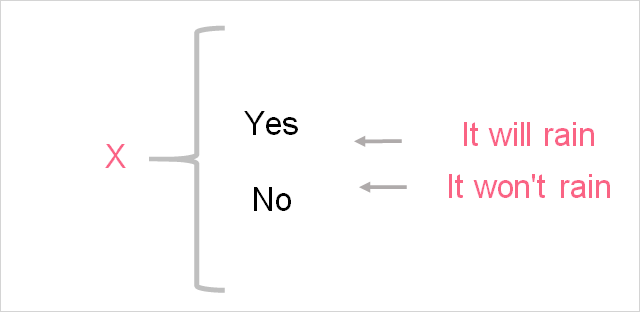
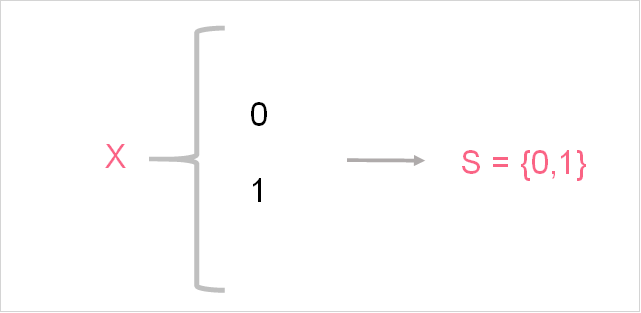
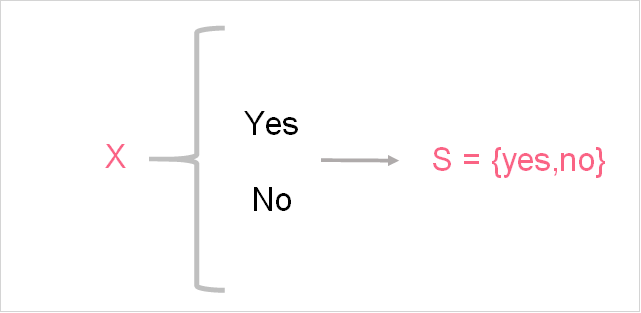
Sample Space
A sample space of any random process is all possible outcomes for that random process. In the example above, there were 2 values in the sample space for flipping a coin: 0 and 1. A sample space typically has the following notation.

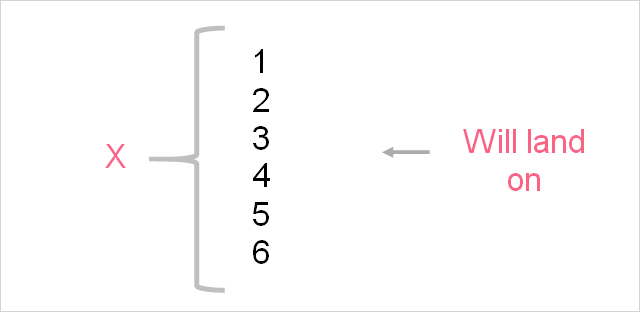
While the previous sample spaces where quite easy to think about, some sample spaces can be a bit more difficult to map out. For example, say you wanted to roll two dice instead of one, what would the sample space be then? In this example, you would have to think about all the possible combinations two dice can result in, starting from one.
| Die 1 | Die 2 | Point in the Sample Space |
| 1 | 1 | {1,1} |
| 1 | 2 | {1,2} |
| 1 | 3 | {1,3} |
| ... | ... | ... |
The total possible combinations of two dice is 36 possible outcomes.
Probability Definition
The probability of an event is how likely that event is to happen. In general, we can talk about events “in probability.” Meaning, how likely are a subset of outcomes given the total sample space.
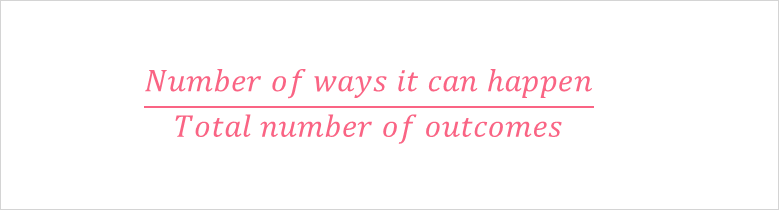
The image above represents the most general formula for probability. Take the coin toss example: what are the chances of the coin landing on heads?

The probability of the coin landing on heads is therefore 0.5, or 50%.
Definition of an Event
In probability theory, an event is simply an outcome or many outcomes of a random experiment. In the previous example, the coin landing on heads or tails was a random event. The random experiment, in this case, would be the actual coin toss. A random experiment is a process whose outcome can’t be known for certain.
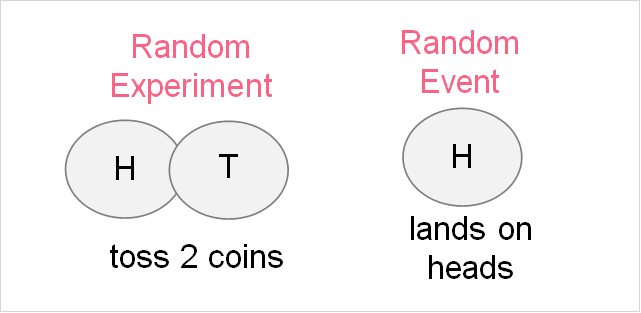
The image above should give you a better idea of the difference between a random event and a random experiment. The definitions are made clearer in the table below.
| Type | Example | Description |
| Random Experiment | Tossing 2 coins | A process or experiment whose outcome is not certain |
| Random Event | Coin lands on heads | A single instance or set of instances of a random experiment |
Types of Events
As explained, an event is a single instance or set of instances of a random experiment. If you’re interested in knowing the probability of a single outcome in the sample space occurring, that is an example of a single event. However, many times, people want to know the probability of a combination of events occurring.
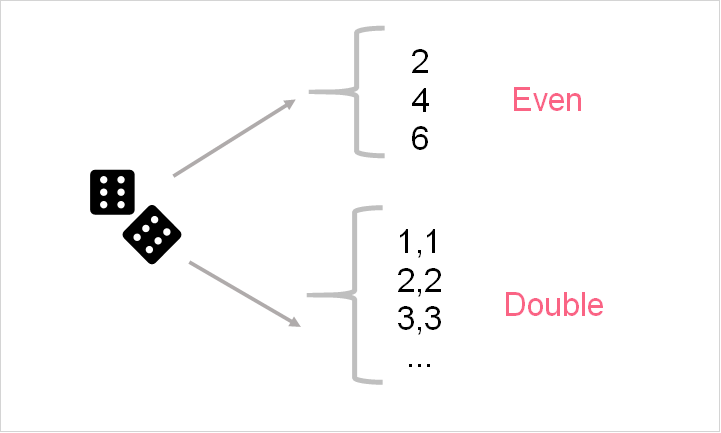
Take the image above as an example. In this random experiment, two dice are being rolled. We’re interested in the likelihood of the event where the dice land on even numbers and where the two numbers are the same. This type of event represents a combination of outcomes.
In probability, you can usually get an indication of what kind of event is being asked about if it includes these words: and, or.
| Type | Symbol | Description |
| And |  | Event A and B both have to occur at the same time |
| Or |  | Either event A or B can occur |
Impossible Event
An impossible event is an event whose probability of occurring is 0. While this may sound silly, it makes more sense with a concrete example. A commonly cited scenario is flipping a coin and getting both heads and tails. If you were to write that in mathematical notation, it would be the following.
| E = heads and tails | The event is flipping a coin and getting heads and tails |
| S = {} | The sample space is empty |
| P(E) = 0 | The probability of event E is 0 |
Sure Event
In contrast with an impossible event, a sure event is one whose probability of occurring is 100%, or 1. This is a bit easier to think about and many examples come to mind. For example, when rolling a die, the event that the die will land on any number from 1 to 6. Because a die only has faces with numbers from 1 to 6, there is a 100% chance that this event will occur.
Compound Event
A compound event should be contrasted against a simple event. A single event is an event that is only 1 value in the sample space. A compound event, on the other hand, can take on multiple values within a sample space. Let’s take the roll of the dice example.
| E = 1 | Single event | The event of the die landing on 1 |
| E = 1,3,5 | Compound event | The event of the die landing on 1, 3 or 5 |
Independent Event
In probability, an independent event is an event whose probability is unaffected by another event. Independent events are typically confused with mutually exclusive events. Mutually exclusive events occur when the probability of one event excludes the probability of another one from happening. To better understand this, let's take a look at the images below.


While the images might seem counter-intuitive, lets break them down with examples, starting with the independent events.
| A = heads | Event A is tossing a coin and landing on heads |
| B = even | Event B is rolling a die and landing on an even number |
| A and B | Tossing a coin to land on heads and rolling a die to land on an even number |
As you can see, the probability of A occurring is unaffected by the occurrence of B because they are independent of each other. However, there is a probability of A and B occurring together. Now, let’s look at an example of a mutually exclusive event.
| A = red | Event A is picking a marble that is red |
| B = blue | Event B is picking a marble that is blue |
| A and B | The probability of picking a marble that is blue and red at the same time is 0 |
As you can see, mutually exclusive events cannot occur at the same time. Another way to call this is disjoint event.
Dependent Event
In contrast, a dependent event is one whose probability is affected by a past event. Let’s go back to our marble example again.

| 1 | A = red | First picking a red marble | P(A) = 2/5 |
| 2 | B = red | Next picking a red marble again | P(B) = 1/5 |
Here, you can see that the probability of event B is directly linked to the outcome of event A.
Complementary Event
In probability, the complement of an event E is the event that E does not happen. The image below makes this notion a bit clearer.














Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian
I’m a junior high school,500 students were randomly selected.240 liked ice cream,200 liked milk tea and 180 liked both ice cream and milktea
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
Where is the answer??
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
ere is a 60% chance that a final years student would throw a party before leaving school ,taken over 50 student from a total of 150 .calculate for the mean and the variance
There are 4 white balls and 30 blue balls in the basket. If you draw 7 balls from the basket without replacement, what is the probability that exactly 4 of the balls are white?