Chapters
In this article, we will discuss what is Bayes' theorem, its general formula and its special case. We will also learn how to use its formula to find the conditional probability. So, let us get started.

What is the Bayes’ Theorem?
The Bayes' theorem is also known as Bayes' rule. In probability theory and statistics, the Bayes' theorem refers to the mathematical formula to find the conditional probability of events. Specifically, Bayes' theorem tells us the probability of an event which is dependent on some initial information of conditions that might be related to that event. Bayes' theorem is named after an English statistician Thomas Bayes. This theorem is the basis of the Bayes' inference. Bayes' theorem is employed in various fields such as medicine, pharmacology, and finance.
Bayes’ Theorem Formula
The following formula is used to express the Bayes' theorem:

Here:
- P (A|B) refers to the probability of the occurrence of an event A, given that event B has already occurred
- P (B|A) refers to the probability of the occurrence of an event B, given that event A has already occurred
- P(A) represents the probability of an event A
- P(B) represents the probability of an event B
You may have noticed that events A and B are independent events, which means that the probability of the result of event A is independent of the probability of the result of event B.
Special Case
There is a special case of Bayes' theorem when event A is a binary variable. In such a case, we use the following formula to compute the probability:
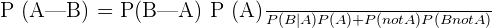
We can have 3 or more cases with A. In this case, we should use the following formula to calculate the probability:
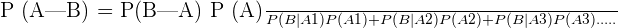
Example 1
There are 3 green and 7 red marbles in a blue bag. Another black colored bag has 8 green and 2 red marbles in it. One marble is drawn at random from one of the bags, which is of the red color. What is the probability that this marble was drawn from the blue bag?
Solution
Suppose A is the probability of selecting a marble from a blue bag and B is the probability of selecting a marble from the black bag.
It means that P(A) = P(B) = 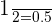
Probability of drawing a red marble from a blue bag = P (R|A) = 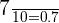
Probability of drawing a red marble from a black bag = P (R|B) = 
We will use the Bayes' theorem to calculate the probability of selecting a red ball from blue bag out of two bags:
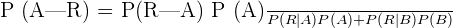
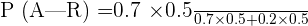
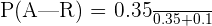

Example 2
A small company has hired two architects to create designs for the clients. Architect 1 makes 65% of the designs and architect 2 makes 35% of the designs. Furthermore, 70% of the designs from architect 1 get approved and 85% of the designs produced by architect 2 get approved. Suppose a design is drawn at random. If the selected design is approved, find the probability that it was made by the architect 2.
Solution
Let 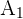 be an event of the design made by the architect 1 and
be an event of the design made by the architect 1 and 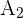 be an event of the design made by the architect 2. Suppose B is an event of selecting an approved design. Now, we will calculate the conditional probability
be an event of the design made by the architect 2. Suppose B is an event of selecting an approved design. Now, we will calculate the conditional probability 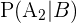 .
.
Use the following formula to calculate this probability:

In this problem, we have:
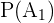 = 0.65
= 0.65
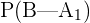 = 0.70
= 0.70
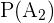 = 0.35
= 0.35
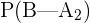 = 0.85
= 0.85
Substitute these values in the formula:

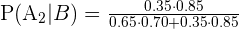
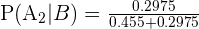



Example 3
John, Alice, and Harry are working in the same company. There is a 25% chance that John will become a manager, 40% chance that Alice will become a manager, and a 35% chance that Harry will become a manager. The probabilities that new rules will be introduced when John, Alice, and Harry will become managers are 20%, 50%, and 40% respectively. If the new rules have been introduced, what is the probability that Harry is the manager?
Solution
Suppose A, B, and C are the events of John, Alice, and Harry becoming managers respectively. Let R be an event that the new rules are introduced. We have to compute the conditional probability P(C|R).
There are 3 cases in this problem, so we will use the following formula:
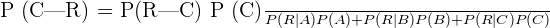
Here:
P(A) = 0.25
P(B) = 0.40
P(C) = 0.35
P (R|A) = 0.20
P (R|B) = 0.50
P (R|C) = 0.40
Now, we will substitute the above values in the formula below to get the probability:
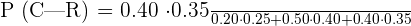
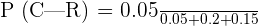
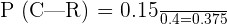
Example 4
In a school, 50% of the students play football and 40% of the boys play basketball. Suppose that 40% of those who play football also play basketball. What percent of those that play basketball also play football?
Solution
Let A be an event of a student playing a football and B be an event of the student playing a basketball.
P(A) = 0.50
P(B) = 0.40
P(B|A) =0.40
Use the Bayes' theorem to calculate percentage of students who play basketball also play football P(A|B).

Substitute the values in the above formula:

= 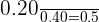
Hence, 50% of the students who play basketball also play football.
Example 5
In a class, 30% of the students like mathematics and 60% of the students like science. Suppose that 20% of those who like mathematics also like science. What percent of those who like science also like mathematics?
Solution
Let A be an event of a student liking mathematics and B be an event of the student liking science.
P(A) = 0.30
P(B) = 0.60
P(B|A) =0.20
Use the Bayes' theorem to calculate percentage of students who like science also like mathematics P(A|B).

Substitute the values in the above formula:
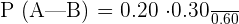
= 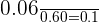
Hence, 10% of the students who like science also like mathematics.













Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian
I’m a junior high school,500 students were randomly selected.240 liked ice cream,200 liked milk tea and 180 liked both ice cream and milktea
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
Where is the answer??
A box of Ping pong balls has many different colors in it. There is a 22% chance of getting a blue colored ball. What is the probability that exactly 6 balls are blue out of 15?
ere is a 60% chance that a final years student would throw a party before leaving school ,taken over 50 student from a total of 150 .calculate for the mean and the variance
There are 4 white balls and 30 blue balls in the basket. If you draw 7 balls from the basket without replacement, what is the probability that exactly 4 of the balls are white?