Chapters
Permutations and combinations tell us different ways in which we can select the objects from a set. Generally, when we solve permutations and combination problems, it is given that the items will be chosen without replacement.
You may be wondering that if both the combinations and permutations are doing the same job, then why different terminologies are used to describe them?
Well, though they perform the same job, however, there is a fundamental difference between these two terminologies. The combination is the selection of items from the set when order is not important. On the other hand, permutation is the selection of items from a group when the order is important. In other words, we can say that permutation is an ordered form of combination.
Let us explain the difference between two terminologies through the following instances:
- This basket has carrots, onions, and potatoes.
- The pin code of my cell phone is 8745.
In the first example, we do not care about the order of three vegetables. We only care about the types of vegetables that are in the basket. Therefore, it is an example of a combination.
In the second example, we have four digits. The pin code will work in the same order exactly. If the order of the digits is changed, then it will not work. Hence, it is an example of permutation.

Permutations Formula
The formula for permutations is given below:
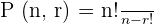
Types of Permutations
There are two types of permutations:
- Permutations with repetitions
- Permutations with no repetition
Permutations with Repetitions
To compute the permutations when repetition is allowed is straightforward. For example, consider the following scenario:
There are "n" different types of objects. It means that we have a choice to select from the"n" number of items. Suppose we are asked to select 4 of the objects from the "n" number of objects. The permutations will be:
n x n x n x n
It means that we will multiply n four times.
Now, let suppose we have to choose m number of items from a collection of n different types. In this case, we will multiply "n" "m" times like this:
n x n x n x n x n x ......(m times)
We can easily write this permutation by employing the exponent of m like this:
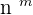
Consider another scenario below:
We select two numbers from the set of the first 100 natural numbers (1, 2, 3, ......100) in such a way that the repetition is allowed. We will write the permutations as:
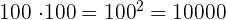
We will get 10,000 permutations.
Hence, we can conclude that the formula for the possible permutations when repetition is allowed is:
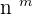
Here:
n reflects the number of objects to select from
m represents the number of objects we want to select
Permutations with no repetition
If all the elements from the set needs to be used or selected then we calculate the permutations by using the formula:

n! is read as n factorial and it is computed by multiplying the numbers from 1 to n together.
Let us consider that in the above example Hannah selects all the pool balls. The number of permutations will be:
8! = 40320
We got the number 40320, like this:
8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40320

Here, n is the number of objects to select from
r represents the number of items we want to select
Now, let us solve some of the examples of permutations.
Example 1.
Calculate P (6,4).
Solution
The formula for computing the permutations is given below:

Substitute n = 6 and r = 3 in the above formula to get the result:



Example 2
Calculate  .
.
Solution
In this case, we don't have the value for r. We only have the value of n. Hence, we can assume that here we will use the formula of permutations when repetition is allowed.

Example 3
Suppose there is a set of 7 chocolates. In how many ways, 4 chocolates can be selected from this set (without repetition)?
Solution
In this example, we are given the following information:
The total number of chocolates = 7
Number of chocolates we want to select = 4
Is repetition allowed = No
The formula for calculating the permutations when no repetition is allowed is given below:
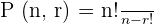
Substitute the values in the above formula to get the number of ways the chocolates can be selected:


Hence, we can select 4 chocolates from a group of 7 chocolates in 840 ways.
Example 4
Suppose there is a set of 9 balls. In how many ways, 5 balls can be selected from this set (without repetition)?
Solution
In this example, we are given the following information:
The total number of balls = 9
Number of balls we want to select = 5
Is repetition allowed = No
The formula for calculating the permutations when no repetition is allowed is given below:
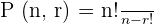
Substitute the values in the above formula to calculate the number of ways the chocolates can be selected:

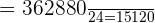
Hence, we can select 5 balls from a set of 9 balls in 15, 120 ways.
Example 5
Suppose there are 4 girls and 3 boys in a classroom. The teacher wants a seating arrangement such that the girls occupy the even places in a row. How many seating arrangements are possible?
Solution
We are given the following information in this problem:
The number of positions = 7
The even positions for girls will be 2, 4, 6, and 8.
The girls can occupy these 4 even places in 4 ways because there are 4 girls:
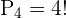
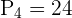
There are 3 positions left which will be occupied by the boys.

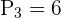
Use the counting principle to compute the number of possible arrangements.
Hence, the total number of seating arrangements possible are:
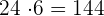













I need to learn
I must say everything is superb I wish I could access to most of my maths topics here! Questions are easy to comprehend. Thanks for your help.
in how many ways can be 5 red balls and green balls be arranged in a row of no two green balls can be next to each other?
Great job but explanations are too complex