1Se lanza un par de dados. Se define la variable aleatoria  como la suma de las puntuaciones obtenidas. Hallar la función de probabilidad, la esperanza matemática y la varianza
como la suma de las puntuaciones obtenidas. Hallar la función de probabilidad, la esperanza matemática y la varianza
Se lanza un par de dados. Se define la variable aleatoria  como la suma de las puntuaciones obtenidas. Hallar la función de probabilidad, la esperanza matemática y la varianza
como la suma de las puntuaciones obtenidas. Hallar la función de probabilidad, la esperanza matemática y la varianza
 | 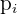 |  |  |
|---|---|---|---|
 | 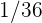 |  | 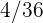 |
 |  | 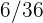 | 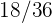 |
 |  | 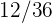 | 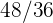 |
 |  | 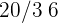 | 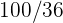 |
 |  |  | 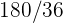 |
 | 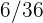 |  | 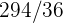 |
 |  | 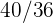 | 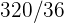 |
 |  |  | 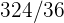 |
 |  |  | 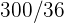 |
 |  |  | 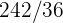 |
 | 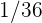 | 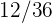 | 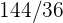 |
 | 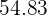 |


2Un jugador lanza un dado corriente. Si sale  o número primo, gana tantos cientos de euros como marca el dado, pero si no sale número primo, pierde tantos cientos de euros como marca el dado. Determinar la función de probabilidad y la esperanza matemática del juego
o número primo, gana tantos cientos de euros como marca el dado, pero si no sale número primo, pierde tantos cientos de euros como marca el dado. Determinar la función de probabilidad y la esperanza matemática del juego
Un jugador lanza un dado corriente. Si sale  o número primo, gana tantos cientos de euros como marca el dado, pero si no sale número primo, pierde tantos cientos de euros como marca el dado. Determinar la función de probabilidad y la esperanza matemática del juego
o número primo, gana tantos cientos de euros como marca el dado, pero si no sale número primo, pierde tantos cientos de euros como marca el dado. Determinar la función de probabilidad y la esperanza matemática del juego
 | 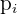 |  |
|---|---|---|
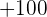 | 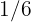 |  |
 | 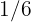 |  |
 | 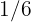 |  |
 | 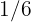 |  |
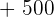 | 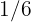 |  |
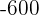 | 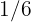 |  |
 |

3Si una persona compra una papeleta en una rifa, en la que puede ganar de  € ó un segundo premio de
€ ó un segundo premio de  € con probabilidades de:
€ con probabilidades de: 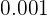 y
y  . ¿Cuál sería el precio justo a pagar por la papeleta?
. ¿Cuál sería el precio justo a pagar por la papeleta?
Si una persona compra una papeleta en una rifa, en la que puede ganar de  € ó un segundo premio de
€ ó un segundo premio de  € con probabilidades de:
€ con probabilidades de: 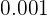 y
y  . ¿Cuál sería el precio justo a pagar por la papeleta?
. ¿Cuál sería el precio justo a pagar por la papeleta?
 €
€
4Sea  una variable aleatoria discreta cuya función de probabilidad es:
una variable aleatoria discreta cuya función de probabilidad es:
 | 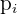 |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
aCalcular la función de distribución.
bCalcular las siguientes probabilidades:



Sea  una variable aleatoria discreta cuya función de probabilidad es:
una variable aleatoria discreta cuya función de probabilidad es:
 | 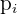 |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
1Calcular la función de distribución.

2Calcular las siguientes probabilidades:









Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
(p)=0,7
Necesito la demostración de que la varianza de una distribucion binomial es n.p.q
Ayuda
una plantacion esta infectada por unos escarabajos y se estima que hay 1,000.000 de estos animalitos se rocia la plantacion con incectisida que se espera que acabe con el 80% de los bichos. ¿ cual es la probabilidad que sobrevivan 500,000?
es 0 no?
me puedes ayudar con este ejercicio por fa
El color de automóviles que los clientes prefieren cambia, al paso de los años y según el modelo en particular que elijan. En el año reciente, 70% de los automóviles de lujo que se vendieron eran negros. Si se elige al azar 20 automóviles de ese año y tipo, encontrar las siguientes probabilidades.
Por lo menos 16 automóviles son negros
Entre 11 y menos de 14 automóviles , son negros
Que 9 automóviles sean negros
Que mas de 5 automóviles no sean negros
Determina la probabilidad para los siguientes experimentos: Si se lanza una moneda y un dado;
A) que caiga sol, par
B) que caiga águila, mayor que 1
C) que caiga sol, menor que 1
Suponga que el 45% de las 40 partes que produce una maquina automática están defectuosas, y que se toma una
muestra de 20 partes al azar con reemplazo, se observa las partes defectuosas. Determinar
a) La función de probabilidad
b) ¿Es posible aproximar a la distribución normal? Demuestre.
Si es posible aproximar a la distribución normal resuelva:
c) La probabilidad de que como máximo 5 resulten defectuosas
d) La probabilidad de que al menos 12 resulten defectuosas.
Ejercicio 1. En un experimento se lanzan 5 monedas y se observa el resultado
(c: cara o s: sello).
a) Encuentre la distribución de probabilidad de la variable aleatoria X: cantidad de caras que se obtienen.
b) Encuentre el valor esperado de la variable aleatoria X, siendo X el número de sellos que se obtienen.
c) Calcule la varianza de la variable aleatoria X, siendo X el número de sellos que se obtienen.
Se lanzan 5 monedas (con cara y sello) y para el lanzamiento se cuenta el número de caras que se observa al lanzar las 5 monedas. Suponga que dicho experimento se repite 1000 veces de forma aleatoria y la siguiente tabla se muestran los resultados:
Número de caras
Frecuencia
0
38
1
144
2
342
3
287
4
164
5
25