Ejercicios de probabilidad condicionada
Sean 
y 
dos sucesos aleatorios con 
, 
, 
.
Determinar:
a 
b 
c 
d 
e 
Sean y dos sucesos aleatorios con , , .
Determinar:
a
Son sucesos dependientes
b
Son sucesos dependientes
c
Son sucesos compatibles
d 
Son sucesos dependientes
En el numerador aplicamos las leyes de Morgan
En el denominador aplicamos la probabilidad del suceso contrario
En el numerador aplicamos la probabilidad del suceso contrario
e
Son sucesos dependientes
En el numerador aplicamos las leyes de Morgan
En el denominador aplicamos la probabilidad del suceso contrario
En el numerador aplicamos la probabilidad del suceso contrario
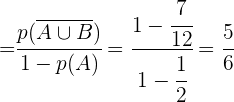
Sean y dos sucesos aleatorios con 
, 
, 
.
Determinar:
a
b
c
d 
e 
f 
Sean y dos sucesos aleatorios con , , .
Determinar:
a
Son sucesos dependientes
b
Son sucesos dependientes
c
Son sucesos compatibles
d 
e 
f 
Problemas de probabilidad condicionada
En un centro escolar los alumnos pueden optar por cursar como lengua extranjera inglés o francés. En un determinado curso, el 
de los alumnos estudia inglés y el resto francés. El 
de los que estudian inglés son chicos y de los que estudian francés son chicos el 
. Eligiendo un alumno al azar, ¿cuál es la probabilidad de que sea chica?
De una baraja de 
cartas se extrae simultáneamente dos de ellas. Calcular la probabilidad de que:
a Las dos sean copas
b Al menos una sea copas
c Una sea copa y la otra espada
De una baraja de cartas se extrae simultáneamente dos de ellas.
Calcular la probabilidad de que:
a Las dos sean copas
Son sucesos dependientes
b Al menos una sea copas
c Una sea copa y la otra espada
Puede salir primero copa y después espada o primero espada y después copa
Ante un examen, un alumno sólo ha estudiado 
de los 
temas correspondientes a la materia del mismo. Éste se realiza extrayendo al azar dos temas y dejando que el alumno escoja uno de los dos para ser examinado del mismo. Hallar la probabilidad de que el alumno pueda elegir en el examen uno de los temas estudiados.
Ante un examen, un alumno sólo ha estudiado de los temas correspondientes a la materia del mismo. Éste se realiza extrayendo al azar dos temas y dejando que el alumno escoja uno de los dos para ser examinado del mismo. Hallar la probabilidad de que el alumno pueda elegir en el examen uno de los temas estudiados.
Una clase está formada por 
chicos y chicas; la mitad de las chicas y la mitad de los chicos han elegido francés como asignatura optativa.
a ¿Cuál es la probabilidad de que una persona elegida al azar sea chico o estudie francés?
b ¿Y la probabilidad de que sea chica y no estudie francés?
Una clase está formada por chicos y chicas; la mitad de las chicas y la mitad de los chicos han elegido francés como asignatura optativa.
a ¿Cuál es la probabilidad de que una persona elegida al azar sea chico o estudie francés?
b ¿Y la probabilidad de que sea chica y no estudie francés?
Un taller sabe que por término medio acuden: por la mañana tres automóviles con problemas eléctricos, ocho con problemas mecánicos y tres con problemas de chapa, y por la tarde dos con problemas eléctricos, tres con problemas mecánicos y uno con problemas de chapa.
a Hacer una tabla ordenando los datos anteriores
b Calcular el porcentaje de los que acuden por la tarde
c Calcular el porcentaje de los que acuden por problemas mecánicos
d Calcular la probabilidad de que un automóvil con problemas eléctricos acuda por la mañana
a Hacer una tabla ordenando los datos anteriores
b Calcular el porcentaje de los que acuden por la tarde.
c Calcular el porcentaje de los que acuden por problemas mecánicos.
d Calcular la probabilidad de que un automóvil con problemas eléctricos acuda por la mañana.
Una clase consta de 
niñas y niños. Si se escoge un comité de tres al azar, hallar la probabilidad de:
a Seleccionar tres niños
b Seleccionar exactamente dos niños y una niña
c Seleccionar por lo menos un niño
d Seleccionar exactamente dos niñas y un niño
a Seleccionar tres niños
b Seleccionar exactamente dos niños y una niña
c Seleccionar por lo menos un niño
d Seleccionar exactamente dos niñas y un niño
Una caja contiene tres monedas. Una moneda es corriente, otra tiene dos caras y la otra está cargada de modo que la probabilidad de obtener cara es de 
. Se selecciona una moneda lanzar y se lanza al aire. Hallar la probabilidad de que salga cara.
Una caja contiene tres monedas. Una moneda es corriente, otra tiene dos caras y la otra está cargada de modo que la probabilidad de obtener cara es de . Se selecciona una moneda lanzar y se lanza al aire. Hallar la probabilidad de que salga cara.
Una urna contiene 
bolas rojas y 
verdes. Se extrae una bola y se reemplaza por dos del otro color. A continuación, se extrae una segunda bola. Se pide:
a Probabilidad de que la segunda bola sea verde
b Probabilidad de que las dos bolas extraídas sean del mismo color
a Probabilidad de que la segunda bola sea verde
b Probabilidad de que las dos bolas extraídas sean del mismo color
En una clase en la que todos practican algún deporte, el 
de los alumnos juega al fútbol o al baloncesto y el 
practica ambos deportes. Si además hay un que no juega al fútbol, cuál será la probabilidad de que escogido al azar un alumno de la clase:
a Juegue sólo al fútbol<\p>
b Juegue sólo al baloncesto<\p>
c Practique uno solo de los deportes<\p>
d No juegue ni al fútbol ni al baloncesto
a Juegue sólo al fútbol
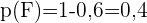
b Juegue sólo al baloncesto
c Practique uno solo de los deportes
d No juegue ni al fútbol ni al baloncesto
En una ciudad, el 
de la población tiene cabellos castaños, el 
tiene ojos castaños y el 
tiene cabellos y ojos castaños. Se escoge una persona al azar:
a Si tiene los cabellos castaños, ¿cuál es la probabilidad de que tenga también ojos castaños?<\p>
b Si tiene ojos castaños, ¿cuál es la probabilidad de que no tenga cabellos castaños?<\p>
c ¿Cuál es la probabilidad de que no tenga cabellos ni ojos castaños?
a Si tiene los cabellos castaños, ¿cuál es la probabilidad de que tenga también ojos castaños?
b Si tiene ojos castaños, ¿cuál es la probabilidad de que no tenga cabellos castaños?
c ¿Cuál es la probabilidad de que no tenga cabellos ni ojos castaños?
En un aula hay 
alumnos, de los cuales: 
son hombres, 
usan gafas, y son varones y usan gafas. Si seleccionamos al azar un alumno de dicho curso:
a ¿Cuál es la probabilidad de que sea mujer y no use gafas?
b Si sabemos que el alumno seleccionado no usa gafas, ¿qué probabilidad hay de que sea hombre?
En un aula hay alumnos, de los cuales: son hombres, usan gafas, y son varones y usan gafas. Si seleccionamos al azar un alumno de dicho curso:
a ¿Cuál es la probabilidad de que sea mujer y no use gafas?
b Si sabemos que el alumno seleccionado no usa gafas, ¿qué probabilidad hay de que sea hombre?
Disponemos de dos urnas: la urna contiene bolas rojas y 
bolas blancas, la urna contiene bolas rojas y bolas blancas. Se lanza un dado, si aparece un número menor que 
; nos vamos a la urna ; si el resultado es ó más, nos vamos a la urna . A continuación extraemos una bola. Se pide:
a Probabilidad de que la bola sea roja y de la urna
b Probabilidad de que la bola sea blanca
a Probabilidad de que la bola sea roja y de la urna
b Probabilidad de que la bola sea blanca
Un estudiante cuenta, para un examen con la ayuda de un despertador, el cual consigue despertarlo en un 
de los casos. Si oye el despertador, la probabilidad de que realiza el examen es 
y, en caso contrario, de 
.
a Si va a realizar el examen, ¿cuál es la probabilidad de que haya oído el despertador?<\p>
b Si no realiza el examen, ¿cuál es la probabilidad de que no haya oído el despertador?
a Si va a realizar el examen, ¿cuál es la probabilidad de que haya oído el despertador?
b Si no realiza el examen, ¿cuál es la probabilidad de que no haya oído el despertador?
En una estantería hay 
novelas y 
libros de poesía. Una persona elige un libro al azar de la estantería y se lo lleva. A continuación otra persona elige otro libro al azar.
a ¿Cuál es la probabilidad de que el libro seleccionado por B sea una novela?<\p>
b Si se sabe que B eligió una novela, ¿cuál es la probabilidad de que el libro seleccionado por A sea de poesía?
a ¿Cuál es la probabilidad de que el libro seleccionado por sea una novela?
b Si se sabe que eligió una novela, ¿cuál es la probabilidad de que el libro seleccionado por sea de poesía?
Se supone que de cada hombres y 
de cada 
mujeres usan gafas. Si el número de mujeres es cuatro veces superior al de hombres, se pide la probabilidad de encontrarnos:
a Con una persona sin gafas<\p>
b Con una mujer con gafas
a Con una persona sin gafas.
b Con una mujer con gafas.
En una casa hay tres llaveros 
y 
; el primero con cinco llaves, el segundo con siete y el tercero con ocho, de las que sólo una de cada llavero abre la puerta del trastero. Se escoge al azar un llavero y, de él una llave para abrir el trastero. Se pide:
a ¿Cuál será la probabilidad de que se acierte con la llave?<\p>
b ¿Cuál será la probabilidad de que el llavero escogido sea el tercero y la llave no abra?<\p>
c Y si la llave escogida es la correcta, ¿cuál será la probabilidad de que pertenezca al primer llavero ?
a ¿Cuál será la probabilidad de que se acierte con la llave?
b ¿Cuál será la probabilidad de que el llavero escogido sea el tercero y la llave no abra?
c Y si la llave escogida es la correcta, ¿cuál será la probabilidad de que pertenezca al primer llavero A?
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
En el ejercicio «Una mesa presidencial está formada por ocho personas. ¿De cuántas formas distintas se pueden sentar, si el presidente y el secretario siempre van juntos?» hay un error en la solución. A mí me sale 10080 = 2×7!
Agradecemos que nos compartieras tu observación. En efecto la solución anterior era para una mesa redonda, ya realizamos la corrección. Un saludo.
Necesito resolver estos problemas de variaciones
V8,5 y V5,3
Supongamos que una escuela deportiva tiene 100 deportistas de los cuales 30 estan en nivel avanzado y 70 estan en nivel intermedio. Si se seleccionan al azar 5 deportistas, calcular la probabilidad de: A. Exactamente de dos de ellos esten en el nivel avanzado B. Exactamente cinco de
En el ejercicio 4 me parece que hay un error, puesto que me da como resultado 70
Una disculpa ya se corrigió.
el ejercicio 3 están mal tomados los datos, a la hora de colocarse en la fórmula se usan datos errados, como el total de la población que posee la enfermedad
Hola , disculpa pero podrias decirme el tema del artículo pues no encuentro el ejercicio que mencionas.
Si tienes razón en tu comentario en cuanto a resolver problemas, pero para tener las capacidades que mencionas es preciso tener experiencia y esa se adquiere resolviendo ejercicios, y se tiene que comenzar a hacerlo con ejercicios sencillos y a medida que se va entiendo el tema se eleva el nivel de los ejercicios hasta poder aplicar los métodos que ya mencionaste.