Temas
Primero, recordemos que las variaciones de  elementos tomados de
elementos tomados de  en
en  están dadas por la fórmula
están dadas por la fórmula
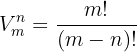
en donde 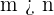 .
.
Igualmente, las variaciones con repetición de  elementos tomando
elementos tomando  están dadas por
están dadas por
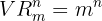
en donde 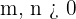 , pero no hay restricciones entre ellos.
, pero no hay restricciones entre ellos.
Una vez recordandas estas definiciones, procedamos con los ejercicios.

Ejercicios aplicados a cifras
1 ¿Cuántos números de tres cifras (todas distintas) se pueden formar con los números  ?
?
Es claro que se tratan de variaciones ya que
1 No entran todos los elementos. Sólo tomaremos tres de los cinco números.
2 Sí importa el orden. No es lo mismo  que
que  .
.
3 No se repiten los elementos. Una vez que tomamos un número este queda fuera de nuestras siguientes opciones, esto sucede ya que todas las cifras deben de ser distintas.
Entonces nos encontramos con variaciones de  elementos tomados de
elementos tomados de  en
en  , esto es,
, esto es,  y
y  , por lo tanto la cantidad de números de podemos formar es
, por lo tanto la cantidad de números de podemos formar es

¿Necesitas clases de apoyo matematicas?
2 ¿Cuántos números de tres cifras (permitiendo cifras repetidas) se pueden formar con los números  ?
?
Es claro que se tratan de variaciones ya que
1 No entran todos los elementos. Sólo tomaremos tres de los cinco números.
2 Sí importa el orden. No es lo mismo  que
que  .
.
3 Sí se repiten los elementos. El mismo ejercicio explica que se permite repetir cifras, esto es, se permiten números como 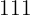 ,
, 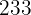 ,
, 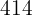 , etc.
, etc.
Entonces nos encontramos con variaciones con repetición de  elementos tomados de
elementos tomados de  en
en  , esto es,
, esto es,  y
y  , por lo tanto la cantidad de números que podemos formar es
, por lo tanto la cantidad de números que podemos formar es

3 ¿Cuántos números de tres cifras (todas diferentes) se pueden formar con los números  ?
?
Notemos que es un caso un poco más complejo, esto ya que el primer dígito tiene que ser estrictamente distinto de cero, por lo tanto tenemos  posibilidades que son los números
posibilidades que son los números 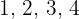 y
y  , esto es, tenemos variaciones de
, esto es, tenemos variaciones de  elementos tomados de
elementos tomados de  en
en 
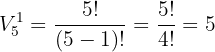
Ahora, una vez que tomamos un número para la primer cifra nos quedarían  números libres más el número
números libres más el número  , ya que la segunda cifra sí puede tomar el valor de
, ya que la segunda cifra sí puede tomar el valor de  , por lo tanto contaríamos de nuevo con
, por lo tanto contaríamos de nuevo con  opciones, entonces para la segunda y tercer cifra ya estamos considerando sobre un conjunto de cinco elementos con la única restricción que no pueden repetirse, por lo tanto tenemos variaciones de
opciones, entonces para la segunda y tercer cifra ya estamos considerando sobre un conjunto de cinco elementos con la única restricción que no pueden repetirse, por lo tanto tenemos variaciones de  tomados de
tomados de  en
en  ya que se cumplen las condiciones
ya que se cumplen las condiciones
1 No entran todos los elementos. Sólo tomaremos dos de los cinco números.
2 Sí importa el orden. No es lo mismo  que
que  .
.
3 No se repiten los elementos.El mismo ejercicio menciona que todas las cifras deben de ser diferentes.
Notemos que para estas variaciones se tiene que  y
y 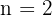 .
.
Así, nuestra solución es la multiplicación de las variaciones para la primer cifra por las variaciones de la segunda y tercer cifra

4 ¿Cuántos números de tres cifras (permitiendo que se repitan) se pueden formar con los números  ?
?
Al igual que el caso anterior es un poco más complejo, esto ya la primer cifra debe de ser ser estrictamente distinta del número cero, por lo tanto tenemos  posibilidades que son los números
posibilidades que son los números 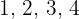 y
y  , esto es, tenemos variaciones de
, esto es, tenemos variaciones de  elementos tomados de
elementos tomados de  en
en 
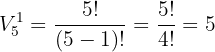
Ahora, una vez que tomámos un número para la primer cifra tenemos que la segunda cifra puede ser cualquiera de los seis números a considerar al igual que la tercer cifra, esto debido a que no tenemos restricciones sobre repetición, por lo tanto tenemos variaciones con repetición de  tomados de
tomados de  en
en  ya que se cumplen las condiciones
ya que se cumplen las condiciones
1 No entran todos los elementos. Sólo tomaremos dos de los cinco números.
2 Sí importa el orden. No es lo mismo  que
que  .
.
3 Sí se repiten los elementos. El mismo ejercicio lo menciona.
Notemos que para estas varciaciones con repetición 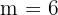 y
y 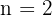 .
.
Así, tenemos que nuestra solución es la multiplicación de las variaciones para la primer cifra por las variaciones con repetición de la segunda y tercer cifra

5 ¿Cuántos números de cinco cifras se pueden formar con los números 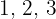 ?
?
Primero notemos que se nos pide formar un número con cinco cifras donde cada cifra solo puede tomar tres valores, esto es 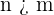 , así que asumimos repetición, ya que de no asumir que los elementos pueden repetirse tendríamos a lo más números con
, así que asumimos repetición, ya que de no asumir que los elementos pueden repetirse tendríamos a lo más números con  cifras. También, notemos que se cumplen las condiciones
cifras. También, notemos que se cumplen las condiciones
1 Entran todos los elementos
2 Sí importa el orden. No es lo mismo  que
que  .
.
3 Sí se repiten los elementos. Es fácil deducirlo.
Así, tenemos variaciones con repetición de  elementos tomando
elementos tomando  , esto es
, esto es 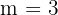 ,
,  , así, la cantidad de números que se pueden formar está dada por
, así, la cantidad de números que se pueden formar está dada por

Ejercicios aplicados a deportes
6 ¿Cuántas quinielas de una columna han de rellenarse para asegurar el acierto de los  resultados?
resultados?
Primero entendamos qué es una quiniela. En la quiniela se tiene una columna en donde hay  juegos, cada juego tiene
juegos, cada juego tiene  posibles resultados, que gane el equipo de la izquierda, que gane el equipo de la derecha o que haya empate. Notemos que entonces estamos tratando con variaciones con repeticiòn en donde
posibles resultados, que gane el equipo de la izquierda, que gane el equipo de la derecha o que haya empate. Notemos que entonces estamos tratando con variaciones con repeticiòn en donde 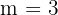 ,
, 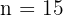 y
y 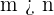 . Además, veamos que
. Además, veamos que
1 Entran todos los elementos.
2 Sí importa el orden. No es lo mismo que gane el equipo de la izquierda a que gane el de la derecha.
3 Sí se repiten los elementos. Es claro que es posible que en dos juegos distintos los respectivos equipos empaten, o que ganen los de la derecha o izquierda.
Así, tenemos que las quinielas a rellenar son

7 ¿De cuántos partidos consta una liguilla formada por cuatro equipos?
Notemos que se cumple lo siguiente
1 Entran todos los elementos.
2 Sí importa el orden. Ya que siempre el equipo de la izquierda se considera "local" y el de la derecha "visitante", esto hace que no sea lo mismo A vs B que B vs A ya que el equipo local y el visitante cambian.
3 No se repiten los elementos.No es posible un partido A vs A.
Así, notemos que tenemos variaciones en donde  y
y 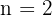 . Dicho esto, lo partidos que se pueden formar son
. Dicho esto, lo partidos que se pueden formar son

8 ¿De cuántas formas diferentes se pueden cubrir los puestos de presidente, vicepresidente y tesorero de un club de fútbol sabiendo que hay  posibles candidatos?
posibles candidatos?
Notemos que se cumple lo siguiente
1 Entran todos los elementos.
2 Sí importa el orden. No es lo mismo que Juan sea presidente y Luis vicepresidente a que Luis sea presidente y Juan vicepresidente.
3 No se repiten los elementos. No es posible que una persona tenga dos puestos distintos.
Así, notemos que tenemos variaciones en donde 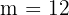 y
y  . Dicho esto, las cantidad de formas distintas en las cuales se pueden cubrir los puestos está dada por
. Dicho esto, las cantidad de formas distintas en las cuales se pueden cubrir los puestos está dada por

Problemas de variaciones en temas diversos
9 A un concurso literario se han presentado  candidatos con sus novelas. El cuadro de honor lo forman el ganador, el finalista y un accésit. ¿Cuántos cuadros de honor se pueden formar?
candidatos con sus novelas. El cuadro de honor lo forman el ganador, el finalista y un accésit. ¿Cuántos cuadros de honor se pueden formar?
Notemos que se cumple lo siguiente
1 Entran todos los elementos.
2 Sí importa el orden. No es lo mismo que María sea la ganadora y Teresa la finalista a que Teresa sea la ganadora y María la finalista.
3 No se repiten los elementos. No es posible que una persona tenga dos puestos distintos en el cuadro de honor.
Así, notemos que tenemos variaciones en donde 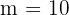 y
y  . Dicho esto, las cantidad de distintos cuadros de honor a formar es
. Dicho esto, las cantidad de distintos cuadros de honor a formar es

10 Con el (punto, raya) del sistema Morse, ¿cuántas señales distintas se pueden enviar, usando como máximo cuatro pulsaciones?
Primero, notemos que al decir que son cuatro pulsaciones como máximo nos dice que debemos considerar cuando solo es una pulsación, cuando son dos, cuando son tres y cuando son las cuatro, por lo tanto debemos considerar cada uno de estos casos y sumarlos todos.
Notemos que cuando es solo una pulsación tenemos solo dos posibles opciones, que sea punto o que sea raya.
Ahora, en general, para cualquier número de número de pulsaciones mayor a  se cumple lo siguiente
se cumple lo siguiente
1 Entran todos los elementos.
2 Sí importa el orden.
3 Sí se repiten los elementos. Podemos tener dos puntos o dos rayas consecutivas
Así, para dos pulsaciones tenemos que la cantidad de señales distintas es

Para tres pulsaciones tenemos que la cantidad de señales distintas es

Para cuatro pulsaciones tenemos que la cantidad de señales distintas es

Así, al final, tenemos que para máximo cuatro pulsaciones la cantidad de señales distintas es
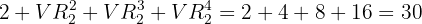
11 Halla el número de capicúas de ocho cifras.
Una capicúa es un número que se lee igual de izquierda a derecha que de derecha a izquierda, por lo tanto, una capicúa tiene la siguiente forma
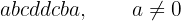
en donde  y
y  son sus cifras. Notemos que en realidad es equivalente a encontrar los distintos números de
son sus cifras. Notemos que en realidad es equivalente a encontrar los distintos números de  cifras que se pueden formar con los dígitos del
cifras que se pueden formar con los dígitos del  al
al  (diez dígitos). En donde
(diez dígitos). En donde  debe de ser estrictamente distinto de
debe de ser estrictamente distinto de  y
y  y
y  pueden tomar cualquier valor, incluyendo el
pueden tomar cualquier valor, incluyendo el  y con repetición, eso es
y con repetición, eso es  puede ser igual a
puede ser igual a  .
.
Pero, ¿cómo lo resolvemos? No es complicado, es igual al ejercicio  . Primero consideremos el caso de
. Primero consideremos el caso de  , notemos que para
, notemos que para  hay
hay  opciones distintas ya que no contamos al
opciones distintas ya que no contamos al  .
.
Ahora, para  ,
,  y
y  tenemos
tenemos  posibilidades para cada uno, entonces, notemos que son variaciones con repetición en donde
posibilidades para cada uno, entonces, notemos que son variaciones con repetición en donde 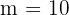 y
y  , donde se cumple que
, donde se cumple que
1 Entran todos los elementos.
2 Sí importa el orden.
3 Sí se repiten los elementos.
Así, las cantidad de formas distintas en las que podemos tomar a  ,
,  y
y  está dada por
está dada por

Para obtener el número de capicúas de  cifras símplemente multipliquemos la cantidad de casos para la primer cifra por la cantidad de casos de la segunda, tercer y cuarta cifra, esto es
cifras símplemente multipliquemos la cantidad de casos para la primer cifra por la cantidad de casos de la segunda, tercer y cuarta cifra, esto es
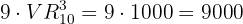
Ecuaciones de combinatoria
12 Resuelve
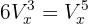
Para resolver simplemente aplicaremos la fórmula de variaciones

De donde se sigue que las soluciones son  y
y  , sin embargo, recordemos que
, sin embargo, recordemos que 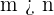 , entonces
, entonces  debe de ser mayor a
debe de ser mayor a  y a
y a  , así, la única solución posible es
, así, la única solución posible es  .
.
13 Resuelve
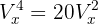
Para resolver simplemente aplicaremos la fórmula de variaciones

De donde se sigue que las soluciones son  y
y  , sin embargo, recordemos que
, sin embargo, recordemos que 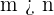 , entonces
, entonces  debe de ser mayor a
debe de ser mayor a  y a
y a  , así, la única solución posible es
, así, la única solución posible es  (además
(además  no puede ser negativo).
no puede ser negativo).
14 Resuelve

Para resolver simplemente aplicaremos la fórmula de variaciones

De donde se sigue que las soluciones son  y
y  , sin embargo, recordemos que
, sin embargo, recordemos que 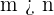 , entonces
, entonces  debe de ser mayor a
debe de ser mayor a  , así, la única solución posible es
, así, la única solución posible es  (además
(además  no puede ser
no puede ser  ).
).
15 Resuelve

Para resolver simplemente aplicaremos la fórmula de variaciones y variaciones con repetición

En este caso la solución es única y es 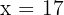 .
.













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Probabilidad de que al lanzar un dado 5 veces salga 3,2,1,5,6,3
De cuántas formas diferentes puedo sentar a 7 personas en dos mesas de 3 y 4 sillas respectivamente?
Muy bueno, solo que, el total d elemento u objetos es la letra ‘n’ y la cantidad de elementos tomados e ‘r’, C(n,r) . El ejmplo excelente. Saludos desde Oruro – Bolivia
Entiendo tu sugerencia pero se usa como total de elementos m yla cantidad de elementos tomados n de n, entonces son letras diferentes pero la idea es la misma, lo que tu sugieres viene en algunos libros, pero lo importante es entender.
En el problema 8, deberíamos esclarecer que la comisión la ocupan 3 alumnos que tienen diferentes cargos en la misma. Sin eso, alguna persona podría pensar que se trata de una combinación y no de una permutación. ya que el orden no importaría si todos tuvieran un mismo rol.
Por lo general cuando se habla de una comisión se piensa que todos ya saben que hay 3 diferentes cargos, pero entiendo lo que sugieres ya que sería más correcto, pero hasta los libros no lo aplican.
de cuantas foras distintas se pueden sentarse 8 personas alrededr de una mesa redonda?pasos para reslverlo por favor