
Área comprendida entre dos funciones
El área comprendida entre dos funciones es igual al área de la función que está situada por encima menos el área de la función que está situada por debajo.
El área encerrada por dos funciones  y
y  viene determinada por la siguiente fórmula:
viene determinada por la siguiente fórmula:

Donde los límites de integración  y
y  corresponden a los puntos de corte entre ambas funciones. Además
corresponden a los puntos de corte entre ambas funciones. Además  debe ser mayor o igual que
debe ser mayor o igual que  . Que una función sea mayor que otra significa que para el mismo rango de valores de
. Que una función sea mayor que otra significa que para el mismo rango de valores de  , el valor de la función es mayor y por tanto su gráfica queda representada por encima en los ejes de coordenadas.
, el valor de la función es mayor y por tanto su gráfica queda representada por encima en los ejes de coordenadas.
Ejemplos resueltos del área entre dos funciones
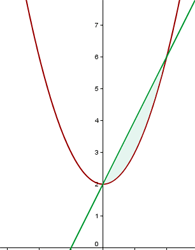
1 Calcular el área del recinto limitado por la parábola 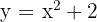 y la recta que pasa por los puntos
y la recta que pasa por los puntos  y
y 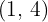 .
.
En primer lugar hallamos la ecuación de la recta que pasa por los puntos indicados: Utilizaremos la forma punto-pendiente para encontrar la ecuación de la recta, para esto encontraremos la pendiente con los puntos dados

Utilizando la forma punto-pendiente

Esto lo haremos al resolver la ecuación
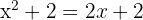
es decir, igualando las funciones
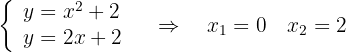
Integrando

2 Hallar el área de la figura limitada por: 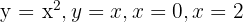
En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites de integración:

entonces
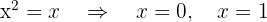

De  a
a  , la recta queda por encima de la parábola
, la recta queda por encima de la parábola

De  a
a  , la recta queda por debajo de la parábola
, la recta queda por debajo de la parábola

entonces
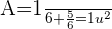
3 Hallar el área de la región del plano limitada por las curvas 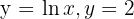 y los ejes coordenados.
y los ejes coordenados.
Calculamos el punto de corte de la curva y la recta 
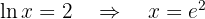
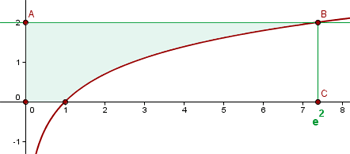
El área es igual al área del rectángulo  menos el área bajo la curva
menos el área bajo la curva  . Tenemos que el área de rectángulo es base por altura, entonces
. Tenemos que el área de rectángulo es base por altura, entonces
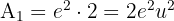
El área bajo la curva  es:
es:

entonces
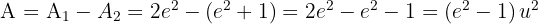
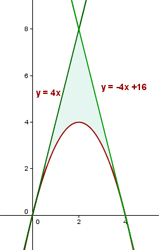
4 Hallar el área del recinto plano y limitado por la parábola  y las tangentes a la curva en los puntos de intersección con el eje OX.
y las tangentes a la curva en los puntos de intersección con el eje OX.
Puntos de intersección con el eje  :
:
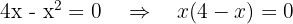
de donde obtenemos que los puntos son  y
y 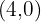 .
.
Ecuación de la tangente a la parábola en el punto 
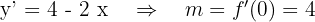
de la forma punto-pendiente de la recta obtenemos que la ecuación es

Ecuación de la tangente a la parábola en el punto 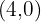
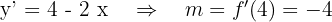
de la forma punto-pendiente de la recta obtenemos que la ecuación es
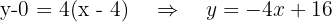
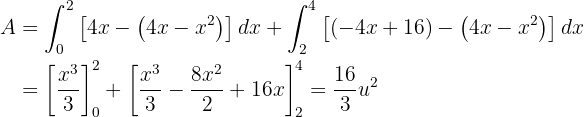
5 Calcular el área limitada por las gráficas de las funciones 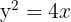 ,
,  .
.
Calculamos los puntos de intersección
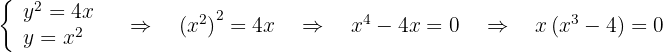
por tanto los puntos de intersección son 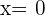 y
y  .
.















Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
en el ejercicio 26 el resultado no se ve bien, como quedaria?
Disculpa pero no hay ejercicio 26, solo llega al 20.
estan la mitad de los ejercicios incorrectos, revisarlos por favor
Podrías indicarnos que ejercicios están mal, pues ya revise y no encontre los errores.
En el ejercicio 13 que es la integral de x^2 * ln(x^2), al hacerlo por partes hace bien lo de coger como u=ln(x^2), pero al coger x^2 como v’ se equivoca y lo coge como x^3
Una disculpa ya se corrigió.
En la pagina no deja ver las respuestas, me parece que es un error de vosotros a ver si lo podeis arreglar, mil gracias
Hola, Pancracio:
Las soluciones ya aparecen correctamente 🙂
Un saludo
Estudio carrera de ingeniería pero me cuesta mucho las matemáticas ¿ algún consejo? O tips