Chapters
You can perform different mathematical operations on vectors which include the addition of vectors. Yes! You can add two or more vectors. In this lesson, you will learn how to add vectors.
Basically, you can't add two vectors, what are doing is adding the components of the vectors with respect to their position. When you add two vectors, it will always result in a single vector that can and can not have the same direction and the same goes for the magnitude as well. In simple words, adding two vectors will result in a new vector in most cases. There are two parts when you are adding vectors, one is the magnitude part which you will do it mathematically. This means with the help of mathematics, you will find the new components of the vector. The second part is the direction, there are two methods to find the direction of the vector and they are the parallelogram method and head to tail method but that is a different story, let's just stick with the addition of components for now.

Adding Magnitude of the Vectors
To add two vectors, add their coordinates or components. For example, you have two vectors that you want to add.

When vector  is added to
is added to  , you need to add the components with respect to their position. For example, you have to add
, you need to add the components with respect to their position. For example, you have to add 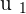 to
to 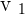 , you can't add
, you can't add 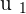 to
to  or
or 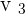 .
.
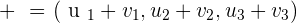
Given  ,
, 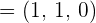 and
and 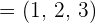 , find the vector
, find the vector  .
.

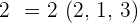


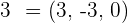

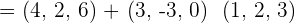

Given vectors 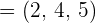 and
and  , determine the magnitude of the vector
, determine the magnitude of the vector  .
.

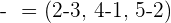
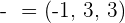

Properties of Vector Addition
Property No.1: Associative
It doesn't matter what way you group, it will always result in the same. In simple words, the way in which the vectors are grouped does not change the result.
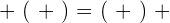
Property No.2: Commutative
The arrangement of vectors (when you are adding) doesn't affect the overall result. In fact, they will always result in the same.
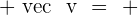
Property No.3: Additive Identity
If you add a null vector to any vector, the result will always remain the same.
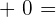
Property No.4: Additive inverse or opposite
If a vector is added to a vector with the same magnitude but in opposite direction, the overall result will always be equal to zero.
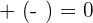
Scalar Multiplication
Scalar multiplication means to multiply a vector with a scalar number. The direction of the vector will remain the same but the length of the vector may vary when you multiply any vector with a scalar number. For example, we have a vector  , now if we multiply the vector
, now if we multiply the vector  by the value
by the value  (which is a scalar number), we will get
(which is a scalar number), we will get  . It means that the vector magnitude has increased three times the size of the previous vector.
. It means that the vector magnitude has increased three times the size of the previous vector.
Basically, there are two conditions for scalar multiplication. The first one is that the number multiplied to the vector should be a scalar quantity. The second condition is that the direction of the vector will never change if you are performing scalar multiplication. Scalar multiplication will not always result in an increase in magnitude, sometimes it can decrease the value of the original vector for example, if you multiply the vector by  , the magnitude of the vector will decrease which will ultimately decrease the length of the vector.
, the magnitude of the vector will decrease which will ultimately decrease the length of the vector.
Properties of Scalar Multiplication
Property No.1: Associative
It doesn't matter what way you group, it will always result in the same. In simple words, the way in which the vectors are grouped does not change the result.

Property No.2: Right distributivity

Property No.3: Left distributivity

Property No.4: Multiplicative identity
This property states that if you multiply any vector with a unit, it will always result in the same vector.

Example
Given  , determine
, determine  so that
so that 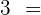 .
.
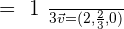
Find more Maths tutors here on Superprof.













