In this article, we will discuss how to compute the scalar triple product of vectors. But before proceeding further, let us define a vector first.
A vector is a quantity that is depicted by magnitude, as well as direction. We represent vectors with alphabets with a right head arrow on the top that depicts their direction. For example,
,
, and
are representations of vectors.
Scalar Triple Product of Vectors
Scalar triple product is also known as a mixed product. The scalar triple product of three vectors ,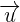 
, and 
is mathematically denoted as 
and it is equal to the dot product of the first vector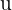 
by the cross product of other two vectors and . It is called a scalar product because similar to a dot product, the scalar triple product yields a single number.
We can denote this product mathematically as:
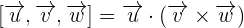
The cross product of these vectors is equal to the determinant. The rows of this determinant are equal to the coordinates of the vectors regarding an orthonormal basis.
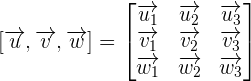
Triple Product Properties
The properties of triple product are given below:
- If the order of the factors is circularly rotated, then the triple product remains unaffected. For instance,
- However, the triple product changes the signs, if the factors are transposed. For instance,
- If three vectors are linearly dependent to each other, then the triple product is equal to zero.
Example 1
Find the scalar triple product of the following vectors:
Solution
Mathematically a scalar triple product is represented as:
First, we will compute the product of 
by using a determinant. The coordinates of these vectors will be the elements of the determinant.
We will calculate the determinant using the formula of finding the determinant of a 3x3 matrix like this:
Now, we will calculate the dot product of 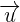and 
like this:
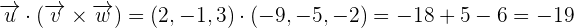
Example 2
Find the scalar triple product of the following vectors:
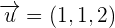
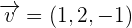
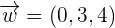
Solution
Mathematically a scalar triple product is represented as:
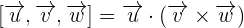
First, we will compute the product of by using determinant. The coordinates of these vectors will be the elements of the determinant.
We will calculate the determinant using the formula of finding the determinant of a 3x3 matrix like this:
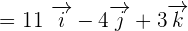
Now, we will calculate the dot product of 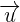and like this:
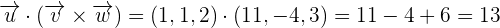
Example 3
Find the scalar triple product of the following vectors:
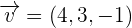
Solution
Mathematically a scalar triple product is represented as:
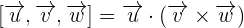
First, we will compute the product of by using determinant. The coordinates of these vectors will be the elements of the determinant.
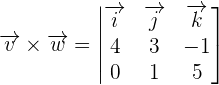
We will calculate the determinant using the formula of finding the determinant of a 3x3 matrix like this:
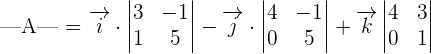
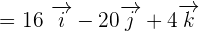
Now, we will calculate the dot product of and like this:
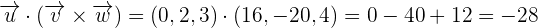
Find more Maths tutor here on Superprof.
Example 4
Find the scalar triple product of the following vectors:
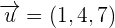
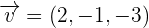
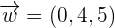
Solution
Mathematically a scalar triple product is represented as:
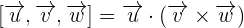
First, we will compute the product of by using determinant. The coordinates of these vectors will be the elements of the determinant.
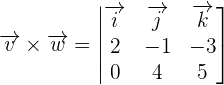
We will calculate the determinant using the formula of finding the determinant of a 3x3 matrix like this:
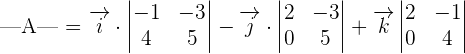
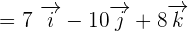
Now, we will calculate the dot product of 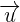and like this:
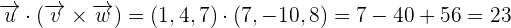
Example 5
Find the scalar triple product of the following vectors:
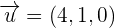
Solution
Mathematically a scalar triple product is represented as:
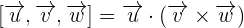
First, we will compute the product of by using determinant. The coordinates of these vectors will be the elements of the determinant.
We will calculate the determinant using the formula of finding the determinant of a 3x3 matrix like this:
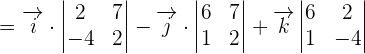
Now, we will calculate the dot product of 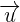and like this:
Did you like this article? Rate it!
Loading...
