Chapters
In this article, we will discuss what is meant by linearly independent vectors and how to tell whether the given vectors are linearly independent or not. But before proceeding to discuss the linear independence of vectors, first, let use define vectors and vector space.
What is a Vector?
A quantity that can be described by the quantity, as well as direction is known as a vector. It is denoted by
.
What is Vector space?
"A vector space refers to a set of objects also known as vectors, that can be added or multiplied by scalar numbers also known as scalars. A vector space is also termed as a linear space"
Most of the time, these scalars are real numbers, however, we do come across the vectors spaces where there is a scalar multiplication by complex or rational numbers. In the next section, we will see what are linearly dependent and independent vectors and how to identify them.
Find more Maths tutor here on Superprof.
Linearly Independent Vectors
In the vectors spaces theory, a set of vectors is believed to be linearly dependent when at least one of the vectors in a set can be expressed as a linear combination of other vectors. On the other hand, the set of vectors is believed to be linearly independent when no vector in a set can be written as a linear combination of any two other vectors. Mathematically, we can denote the concept as:
There are different directions of linearly independent vectors and their components are not proportional to each other. If linearly independent vectors are written in the matrix form, then the determinant of the matrix is non zero. On the other hand the determinant of the linearly dependent matrix is zero.
Now, we will solve some examples in which we will determine whether the given vectors are linearly independent or dependent.
Example 1
Determine whether the following vectors are linearly dependent or independent.
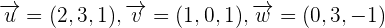
Solution
Multiply the vectors u, v and w with a, b and c respectively in such a way that a + b + c = 0.
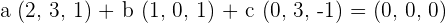
Write the above equation as system of equations like this:
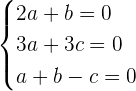
Recall the formula for finding the determinant of the 3 x 3 matrix and use it to calculate the determinant of the above matrix because it has 3 rows and 3 columns.
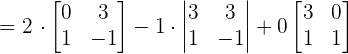
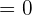
Since the determinant is zero, so the vectors are linearly dependent.
Example 2
Demonstrate whether the vectors 
are linearly dependent or independent.
Solution
First, we will multiply a, b and c with the vectors u , v and w respectively:
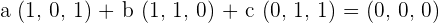
Now, we will write the above equation as system of linear equations like this:
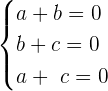
Now, we will write the equations in a matrix form to find the determinant:
Find the determinant using the formula of 3 x 3 determinant:
Since the determinant is non zero, therefore the vectors are linearly independent.
Example 3
Demonstrate whether the vectors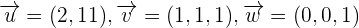 
are linearly dependent or independent.
Solution
First, we will multiply a, b and c with the vectors u , v and w respectively:
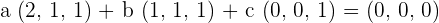
Now, we will write the above equation as system of linear equations like this:
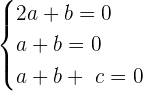
Now, we will write the equations in a matrix form to find the determinant:
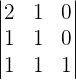
Find the determinant using the formula of 3 x 3 determinant:
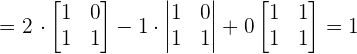
Since the determinant is non zero, therefore the vectors are linearly independent.
Example 4
Determine whether the vectors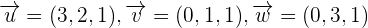 
are linearly dependent or independent.
Solution
First, we will multiply a, b and c with the vectors u , v and w respectively:
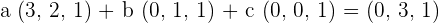
Now, we will write the above equation as system of linear equations like this:
Now, we will write the equations in a matrix form to find the determinant:
Recall the formula of finding the determinant of a 3x3 matrix and use it to find the determinant of the above matrix:
Since the determinant is non zero, therefore the vectors are linearly independent.
Example 5
Demonstrate whether the vectors 
are linearly dependent or independent.
Solution
First, we will multiply a, b and c with the vectors u , v and w respectively:
Now, we will write the above equation as system of linear equations like this:
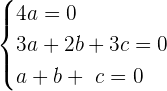
Now, we will write the equations in a matrix form to find the determinant:
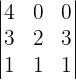
Recall the formula of finding the determinant of a 3x3 matrix and use it to find the determinant of the above matrix:
Since the determinant is non zero, therefore the vectors are linearly independent.
Example 6
Determine whether the vectors 
are linearly dependent or independent.
Solution
First, we will multiply a, b and c with the vectors u , v and w respectively:
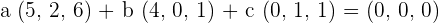
Now, we will write the above equation as system of linear equations like this:
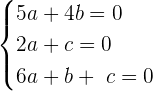
Now, we will write the equations in a matrix form to find the determinant:
Find the determinant using the formula of finding the determinant of a 3 x 3 matrix:
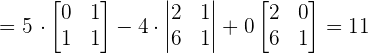
Since the determinant is non zero, therefore the vectors are linearly independent.
Did you like this article? Rate it!
Loading...
