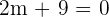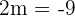Chapters
Like addition and subtraction, you can multiply vectors as well. There are two ways to multiply vectors and both are different. One is the dot product, which is also known as the scalar product of vectors, and the other one is the cross product. As mentioned before, the dot product differs a lot from cross-product but in this lesson, we will cover only the dot product.
Vectors depend on their magnitude and direction. What matters is the data we require, sometimes, our only concern is with the direction, sometimes magnitude, and sometimes both. When you do dot product of two vectors, you are basically projecting one vector onto another. For example, you have two vectors, vector  and vector
and vector 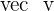 and our area of concern is how much the vector
and our area of concern is how much the vector  is pointing in the same direction as the vector
is pointing in the same direction as the vector 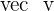 . What we are looking for is whether the quantity is positive, negative, or zero. Each quantity has meaning. If the quantity is zero, that means both vectors are perpendicular, on the other hand, if the quantity is positive, that means both vectors are in a similar direction. Last but not least, if the dot product is negative, that means both vectors are in opposite directions.
. What we are looking for is whether the quantity is positive, negative, or zero. Each quantity has meaning. If the quantity is zero, that means both vectors are perpendicular, on the other hand, if the quantity is positive, that means both vectors are in a similar direction. Last but not least, if the dot product is negative, that means both vectors are in opposite directions.
The dot product is specifically called scalar product because of a special reason. The reason is that the result of the dot product will always be scalar. It is basically the multiplication of both vector's magnitude with their angle. The direction doesn't play an important role here because our concern is with the magnitude only. Although, the result indicates the direction of the vector, the science behind the dot product is that their magnitudes are multiplying but then what is the direction part? How does the answer to dot product help us to find the direction of both vectors? It is the cosine part of the dot product. The cosine part helps in determining the direction of both vectors.
In nutshell, the dot product or scalar product of two vectors is the product of their magnitudes multiplied by the cosine of the angle that they form.

It can also be expressed as:
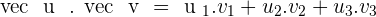
Example
Find the dot product of two vectors whose coordinates in an orthonormal basis are:  and
and 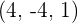 .
.


Magnitude of a Vector
Finding magnitude is the most important part of the dot product. In fact, dot product is the multiplication of magnitudes of both vectors. If you don't know how to find the magnitude of a vector then finding dot product will be impossible. To find the magnitude of a vector, you need its components. These components can be obtained with the help of a standard basis and unit vectors. Let's say you have a vector 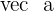 and you found its components,
and you found its components, 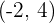 (in this example, we are considering only 2D vectors). The next step is to use the magnitude formula to find the magnitude. The magnitude of avector is represented like this
(in this example, we are considering only 2D vectors). The next step is to use the magnitude formula to find the magnitude. The magnitude of avector is represented like this 
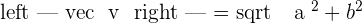
Where a and b represent components of a vector. For the above example, we will be writing like this:

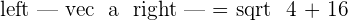
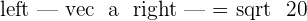
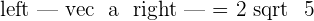
Let's have a close look up at the dot product formula:

It requires both vector's magnitude which means we need to find both vector's magnitude to find the dot product. For that, you need to find the magnitude of the vector 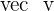 separate and you have to do the same for the
separate and you have to do the same for the  too and then multiply both.
too and then multiply both.

Example
Find the magnitude of a vector with coordinates 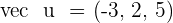 in an orthonormal basis.
in an orthonormal basis.
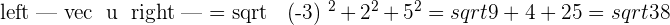
Angle between Two Vectors
Dot product allows you to find the angle between two vectors as well. Below is the formula and if you want to learn in detail how this formula came into life then click here.

Example
Determine the angle between the vectors  and
and 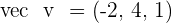 .
.

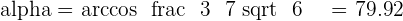 °
°
Orthogonal Vectors
Two vectors are orthogonal or perpendicular if their dot product is zero.
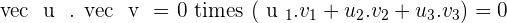
Example
Calculate the x and y values for the vector  that is orthogonal to the vectors
that is orthogonal to the vectors 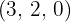 and
and 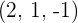 .
.
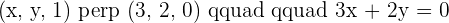


Properties of the Dot Product
Commutative
The arrangement of the vectors will not change the overall result. In simple words, it doesn't matter in what order you arrange vectors, they will always result the same.
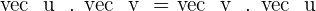
Associative
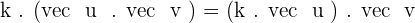
Distributive

4
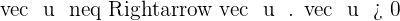
Geometric Interpretation of the Dot Product
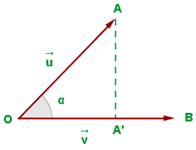
Scalar Projection
Scalar projection is basically the magnitude of the vector projection. It is the projection when you dot product the unit vector with the vector in a particular direction. If the scalar projection results in a positive value that indicates the angle between both vectors is less than 90∘. It also means that both vectors are in the same direction. On the other hand, if the scalar projection results in a negative value, that indicates the angle between both vectors is greater than 90∘. This also tells us that the vectors are in opposite directions.
Find various Maths teacher on Superprof.
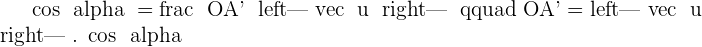
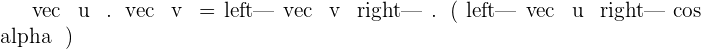


Vector Projection
The vector projection is the unit vector of 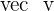 by the scalar projection of u on v. In mathematical language, this is written as
by the scalar projection of u on v. In mathematical language, this is written as 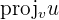 . It means that the vector "v" is projected onto "u". In simple words, a new vector is projected and in the direction of u. Vector projection is frequently used in physics and maths.
. It means that the vector "v" is projected onto "u". In simple words, a new vector is projected and in the direction of u. Vector projection is frequently used in physics and maths.


The scalar projection of u on v is the magnitude of the vector projection of u on v.
Exercise
Given the vectors 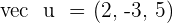 and
and  , calculate:
, calculate:
1. The magnitudes of  and
and 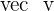 ·
·
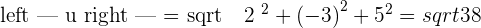
 °
°
2. The dot product of  and
and 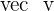 ·
·

3. The angle.
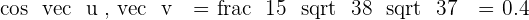
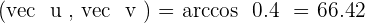
4. The value of m for which vectors 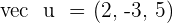 and
and 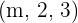 are orthogonal.
are orthogonal.