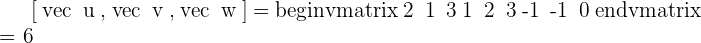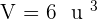Chapters

Exercise 1
Given the vectors 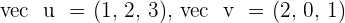 and
and 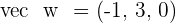 , calculate the following:
, calculate the following:
1. 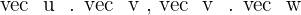
2. 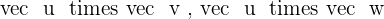
3. 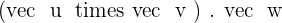
4. 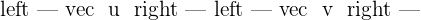
5. 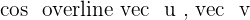
Exercise 2
For what values of a do the vectors 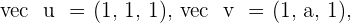 and
and 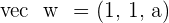 form a basis?
form a basis?
Exercise 3
Determining the value of the coefficient k for the vectors 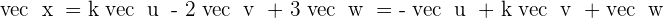 if the vectors are:
if the vectors are:
1. Orthogonal.
2. Parallel.
Exercise 4
Find the direction cosines of the vector 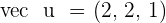 .
.
Exercise 5
Calculate the angle between the vectors 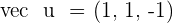 and
and 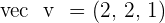 .
.
Exercise 6
Given the vectors  and
and 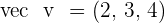 , calculate:
, calculate:
1 The magnitudes of  and
and 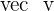 ·
·
2 The cross product of  and
and 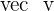 ·
·
3 The unit vector orthogonal to  and
and 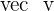 ·
·
4 The area of the parallelogram whose sides are the vectors  and
and 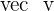 ·
·
Exercise 7
Calculate the triple product of: 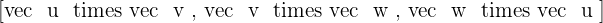 if
if 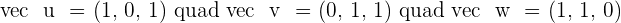 .
.
Exercise 8
Given the vectors 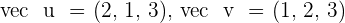 , and
, and 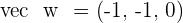 , calculate the triple product
, calculate the triple product 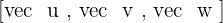 . Also, what is the volume of the parallelepiped whose edges are formed by these vectors?
. Also, what is the volume of the parallelepiped whose edges are formed by these vectors?
Solution of exercise 1
Given the vectors 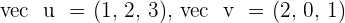 and
and 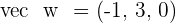 , calculate the following:
, calculate the following:
1. 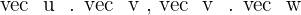
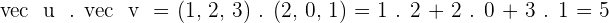

2. 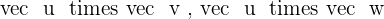
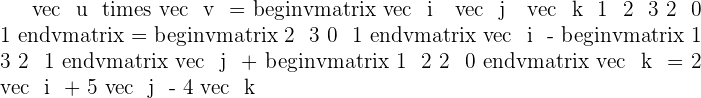

3. 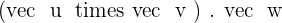

4. 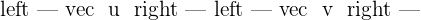
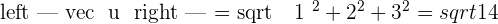
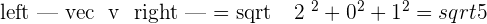
5. 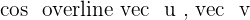

Solution of exercise 2
For what values of a do the vectors 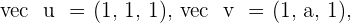 and
and 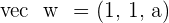 form a basis?
form a basis?
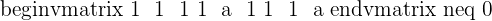

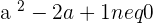
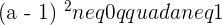
For 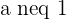 , the vectors form a basis.
, the vectors form a basis.
Solution of exercise 3
Determining the value of the coefficient k for the vectors 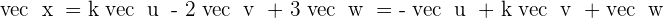 if the vectors are:
if the vectors are:
1. Orthogonal.
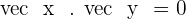


2. Parallel.

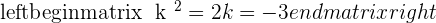
The system does not have a solution.
Solution of exercise 4
Find the direction cosines of the vector 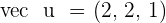 .
.
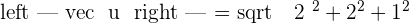
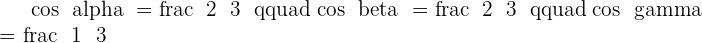
Find various Maths tutors near me on Superprof.
Solution of exercise 5
Calculate the angle between the vectors 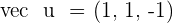 and
and 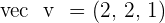 .
.
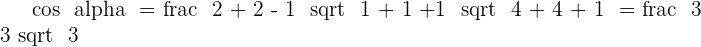

Solution of exercise 6
Given the vectors  and
and 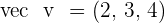 , calculate:
, calculate:
1 The magnitudes of  and
and 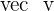 ·
·
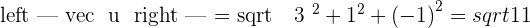
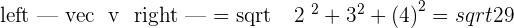
2 The cross product of  and
and 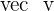 ·
·

3 The unit vector orthogonal to  and
and 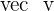 ·
·

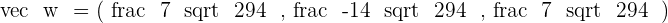
4 The area of the parallelogram whose sides are the vectors  and
and 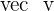 ·
·

Solution of exercise 7
Calculate the triple product of: 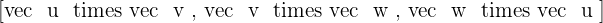 if
if 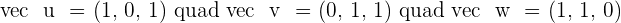 .
.
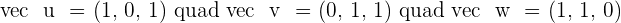
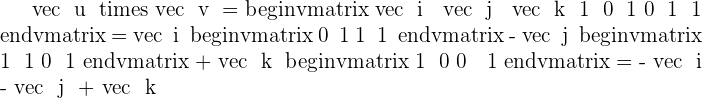


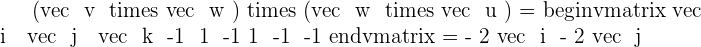
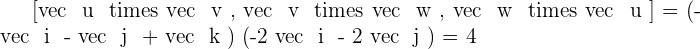
Solution of exercise 8
Given the vectors 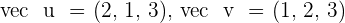 , and
, and 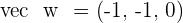 , calculate the triple product
, calculate the triple product 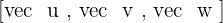 . Also, what is the volume of the parallelepiped whose edges are formed by these vectors?
. Also, what is the volume of the parallelepiped whose edges are formed by these vectors?