We live in a 3-dimensional world which means we have 3 axes as reference. Those axes are the x-axis, y-axis, and z-axis. Vector knowledge is applicable in real life which ultimately means that all vector laws are applied but in previous resources, we were stuck to 2-dimension, does the 3-dimensional world changes all laws? Absolutely! but is that change too big? No, all you will be doing is adding the third dimension (which is the z-axis) to all those laws. A 3D vector is a line segment in three-dimensional space running from point A (tail) to point B (head).
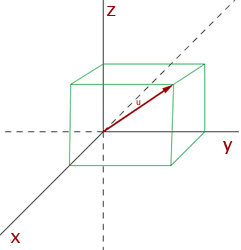
Each vector has a magnitude (or length) and direction. Remember, the fundamentals will not change because we are just adding another dimension here. It doesn't mean that what you have studied before will be changed totally, just a few changes in the formula but the concept will remain the same. If you have a good understanding of previous laws then understanding laws in 3-dimensions will not be a problem for you.
Components of a 3D Vector
When we are working in a 3 dimension space, we always consider all three coordinate bases which are the x-axis, y-axis, and z-axis. For example, we have two points in the 3 dimension space and they are point A and point B. The coordinate of point A and B will be written (in 3 dimension space) like this: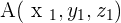 
and 
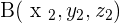. Your teacher also asked you to find the vector 
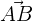but in the 3 dimension space then how will you do it? Is it the same head minus the tail? Yes, exactly it is the same! You need to subtract the head coordinate from the tail coordinate.
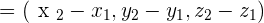
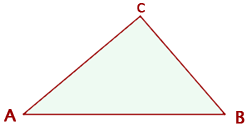
Calculate the components of the vectors that can be drawn in the triangle with vertices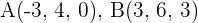 
and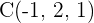 
.
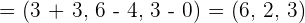
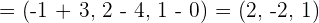
Don't forget that vector consists of two things, one is the direction and other is the magnitude. If you reverse the direction that means all the coordinates of the vector will also be reversed:
Magnitude or Length of a Vector
Magnitude is the key element of a vector and a vector without magnitude is just a direction with no power. The magnitude of a vector is the length of the line segment that defines it. The magnitude of a vector is always represented by a positive number and only the zero vector has a magnitude of zero.
Calculation of the Magnitude to Know Its Components
You might be familiar with magnitude formula which is 
but with a third new dimension, things will be a bit different. To find magnitude of a 3 dimension vector, you need to sum all the squared components of different axis and then take a square root of the answer.
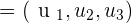
Below is a solved question for more clarification.
Given the vectors 
and 
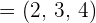, find the magnitudes of 
and 
·
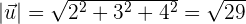
Calculation of the Module Knowing the Coordinates of the Points
To calculate magnitude, we will use the distance formula but with a small change. You might have encountered 2 dimension problems before and that is why you were using just x and y components at that time but things have changed now. This time, you will be using three components but don't worry, if you have a good understanding of the distance formula, this will be a piece of cake for you. For example, you have two points A and B. The coordinates of A are 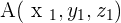and the coordinates of B are .
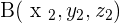The first step is to subtract the tail component from the head component like you used to do it previously. Find the difference for all the components and then take a square of all those answers. Add all those squared answers and then take a square root of the resultant answer and that is your magnitude of two different vectors or you can use the below formula and just plug in the values and find the answer in just one step.
Distance between Two Points
The formula for distance between two point is same as the finding magnitude of two vectors.
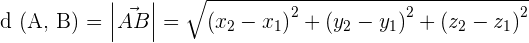
EXAMPLE
Find the distance between points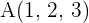 
and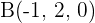 
.
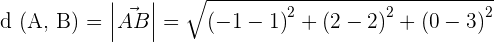
Unit Vector
Vectors come in all kinds of shapes and sizes but how do we describe those vectors? With the help of the unit vector. The definition of the unit vector is pretty simple, it is a vector that has a magnitude of 
. This means that any vector which has a magnitude of one, irrespective of direction, is called a unit vector. One of the most common terms we use in the chapter on vectors is called normalizing. Normalizing means obtaining another unit vector in the same direction. To normalize a vector, you need to divide the components of that vector by the magnitude of the vector.
Find various Maths tutor near me on Superprof.
Did you like this article? Rate it!
Loading...
