What is a Vector?
A vector is a quantity that has magnitude and a direction. It means that both things are necessary for a vector. Without direction, a vector will be a straight line, without magnitude, a vector won't even exist. We denote vectors on the basis of head and tail. Basically, a vector is a line segment running from point A (tail) to point B (head).
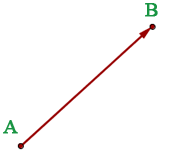
Whenever we draw a vector, we draw it from its tail to its head. The tail represents the starting point of the vector and the head is the finishing point of the vector. The direction is represented by the head of the vector and that is why we draw an arrow pointing in the specific direction on the head of the vector. The length represents the magnitude so in slang language, the longer the vector, the higher the magnitude.
Properties of a Vector
Direction of a Vector
This is the direction of the line which contains the vector or any line which is parallel to it.
Magnitude of a Vector
The magnitude of the vector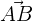 
is the length of the line segment 
. It is denoted by 
.
The magnitude of a vector is always a positive number or zero because matter is always positive, you can't turn positive 1kg rice to negative 1kg rice, can you? Does this mean that the vector can't be negative at all? Is vector a positive entity? No, a vector can have a negative sign so what does it mean? It represents the direction. If you look at the standard axis, the more you go from left to right, the more positive values you will see and if you move from right to left, you will see a transition of positive values to negative values, and possibly you might not even see a positive value when moving left. Vectors work the same, basically, the negative sign works according to the axis which means the axis becomes the frame of reference for a vector. A vector can have its own frame of reference too and to explain that it deserves its own separate blog about it, let's stick to the direction and magnitude of vector for now.
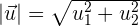
The magnitude of a vector can be calculated if the coordinates of the endpoints are known:
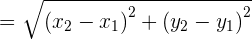
Calculate the magnitude of the following vectors:
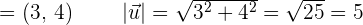
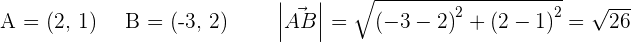
Calculate the value of k knowing the magnitude of the vector 
is 5.
Types of Vectors
Position Vector
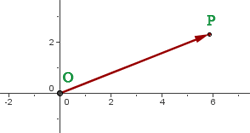
The vector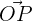 
that joins the origin coordinates, O, with a point, P, is the position vector of the point P
Components or Coordinates of a Vector
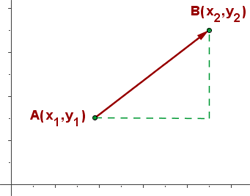
Find the components of the vector :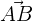
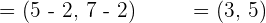
The vector 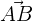has the components 
. Find the coordinates of A if the terminal point is known as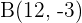 
.
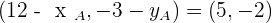
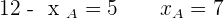
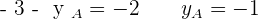
Hence,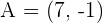 
Calculate the coordinates of point D so that the quadrilateral of Points: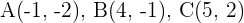 
, and D form a parallelogram.
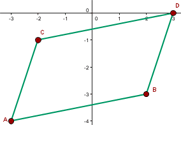
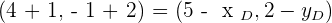
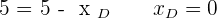
Hence,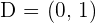 
Find more Maths tutors here on Superprof.
Did you like this article? Rate it!
Loading...
