Chapters
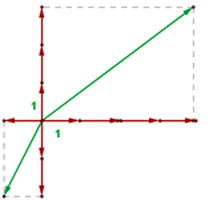
Vector has magnitude and direction. The direction of a vector can be identified by its arrow but what about the magnitude? To find the magnitude of a vector, you need to know its components but then how do we find the components of the vector? That is where we use the standard basis to find the components of a vector. The standard basis vectors mean that vectors are defined with respect to their axes. For example, we have a vector named 
. Vector has a direction but we are interested in its magnitude and to find the magnitude, we need its components. That is where we will use the axes to find the value of the vector coordinates. By drawing the vector on the axes, we can easily find the value of the coordinates of the vector .
The way the axes are distributed can be changed, that is the beauty of the standard basis. In easy words, you can choose any basis you want. For example, you can choose 2 units to represent one on the x-axis and one unit to represent 2 on the y-axis. On the other hand, no matter what standard basis you choose, they will be written like this:
Two linearly independent vectors, 
and form a basis because any vector in the plane can be set as a linear combination of them.
The components of the vector that form the basis are:
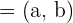
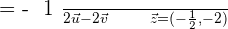
However, two vectors that form a basis cannot be parallel to one another.
Example
Which pairs of the following vectors form a basis?
For vector u and v:
For vector v and w:
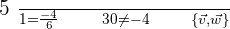
For vector u and w:
Orthogonal Basis
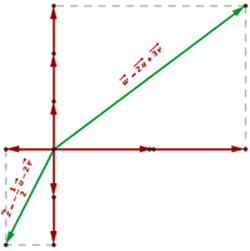
The two basis vectors are mutually perpendicular.
Orthonormal Basis
The two basis vectors are mutually perpendicular and their magnitude is one.
Find more Maths tutor here on Superprof.
Standard Basis
The base formed by 
and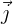 
is called the standard basis or canonical basis.
The standard basis is the base that is commonly used, so if nothing is noticed, it should be working on that basis.
Given the vectors 
, 
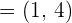and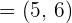 
.
1. Determine if and 
form a basis.
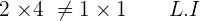
2. Express as a linear combination.
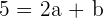
After solving both equations simultaneously, we will get:
3. Calculate the coordinates of with respect to the base.
The coordinates of with respect to the base are: 
.
A vector has coordinates 
in the standard basis. Which coordinates of will be referred to the basis of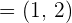 
, 
?
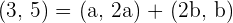
Dividing for single coordinates:
Using the first equation and making it in terms of "a":
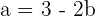
Plugging the value of a in the equation no.2:
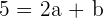
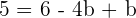
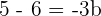
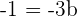
Plugging the value of b in the equation no.1:
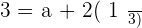
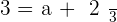
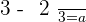
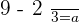
The coordinates of in the basis B are 
Did you like this article? Rate it!
Loading...
