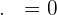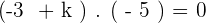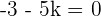The concepts of orthogonal and orthonormal vectors are pretty easy to understand. These concepts are applied when you are performing dot product on two vectors. Hence, when you apply dot product, you will either get orthogonal vectors are orthonormal vectors.
Orthogonal Vectors
Two vectors are orthogonal or perpendicular if their dot product is zero. This means that both vectors are perpendicular to each other because the 
component becomes zero when the angle between both vectors is 
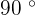and when is zero that means the dot product of both vectors is zero.
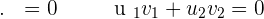
Example
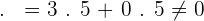
Not perpendicular which means both vectors are also not orthogonal.
Orthonormal Vectors
Two vectors are orthonormal if:
1. Their dot product is zero.
2.The two vectors are unit vectors.
One of the most frequently asked questions is the difference between orthonormal and orthogonal vectors. Orthonormal vectors are the same as orthogonal vectors but with one more condition and that is both vectors should be unit vectors. If both vectors are not unit vectors that means you are dealing with orthogonal vectors, not orthonormal vectors.
Find more Maths tutor here on Superprof.
Examples
Q.1 Calculate the value of k for the vectors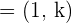 
and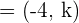 
knowing that they are orthogonal.
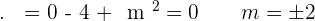
Q.2 If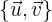 
is an orthonormal basis, calculate:
1 
2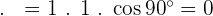 
3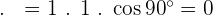 
4 
Q.3 If 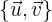is an orthonormal basis and 
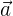and 
are:
Q.4 Calculate the value of k knowing that 
.
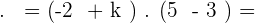
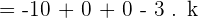
Q.4 If 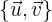is an orthonormal basis and 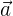and are:
Q.5 Calculate the value of k for the two orthogonal vectors.
Did you like this article? Rate it!
Loading...
