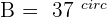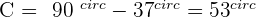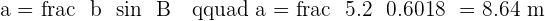The word triangle can be broken into two words, one is the tri another is the angle. It means that a triangle is a geometry that has just three angles. To make a geometry for just three angles, mathematicians found that it would also need three sides. That is how a triangle was born and today, it helps a lot in many applications. There are many types of triangles and each triangle has a different property that makes it more valuable to us. There are three types of primary triangles that mathematicians have categorized:
- Equilateral Triangle
- Isosceles Triangle
- Scalene Triangle
In this lesson, our main focus will be on solving right-angle triangles but in the above list, we mention the right-angle triangle, right? The above list is a list of primary triangles which means all other triangles are derived from them and the right-angle triangle is no exception. The right-angle triangle is a type of Isosceles triangle because in a right-angle triangle, one of the angles is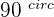 
that means the remaining angles will be equal as well. This isn't always the case, in many cases, other angles are different but still, it is considered to be an Isosceles triangle because of the 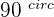angle. In simple words, a right triangle has a right angle 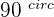and two acute angles.
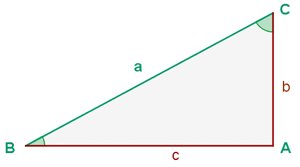
Right angle triangle consists of two parts. These parts are very important to understand because many theorems and laws applied to the right-angle triangle require an understanding of these parts. Below are the parts of a right-angle triangle with its detail.
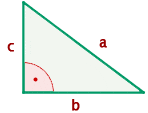
Hypotenuse
The hypotenuse is the side opposite the right angle and is the largest side of the triangle. Please do note that hypotenuse is not the height of the right-angle triangle.
Legs or Catheti
The legs or catheti (singular: cathetus) are the sides opposite the acute angles and are the shorter sides of the triangle.
Pythagorean Theorem
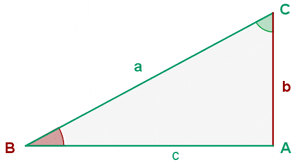
Pythagorean theorem states that in a right triangle, the square of the hypotenuse equals the sum of the squares of the legs. The only condition of the Pythagorean theorem is that it is only applicable to right-angle triangles. It means that if the triangle is not a right-angle triangle then this law can't be applied. To understand this law properly, we named all the sides of the right-angle triangle.
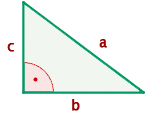
The angle between c and b is 
hence the opposite of angle will be the hypotenuse which is denoted by a. Since the square of the hypotenuse is equal to the sum of squares of the leg that means the hypotenuse is on the other side of the equation and remaining will be on the next to that equation like this:
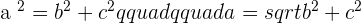
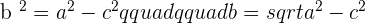
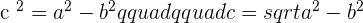
Area of a Right Triangle
The area of a right triangle is equal to half the product of the legs.
Solving Right Triangles
To solve a triangle, we must find the value of all the sides and angles.
To solve a right triangle, we will use trigonometric ratios as well as the Pythagorean theorem.
1. The Hypotenuse and a Leg Are Known
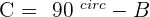
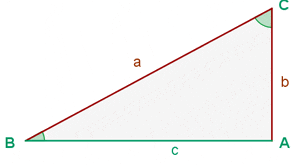
Example
Solve a right triangle knowing:
and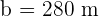 
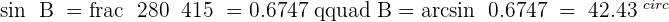
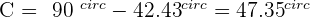
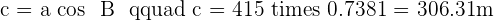
2. Two Legs Are Known
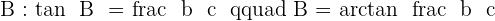
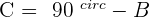
Example
Solve a right triangle knowing:
and 
.
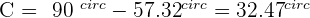
3. The Hypotenuse and an Acute Angle Are Known
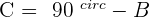
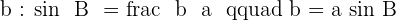
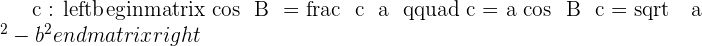
Example
Solve a right triangle knowing:
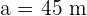and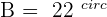 
.
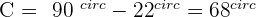
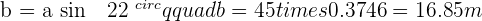
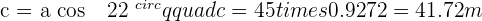
4. A Leg and an Acute Angle Are Known
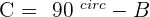
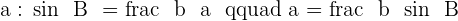
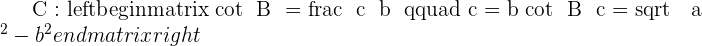
Example
Solve a right triangle knowing:
and 
Did you like this article? Rate it!
Loading...
