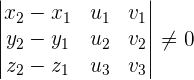The intersection of two or more lines plays a very important role in geometry. When we talk about the intersection, we mainly talk about roots or solutions. However, there are many types of correlation lines. We usually not talk about it because our concern was up to finding the roots or solutions of the equations of those lines. This doesn't mean that it is not that important, as a matter of fact, you should know how lines are intersecting with each other. In this blog, you will learn different correlations and how you can find them.
Lines Defined by Two Planes
You might be familiar with graphs that have ordinate and abscissa only. However, those graphs are known as a 2-dimensional graph. We live in a world that is 3-dimensional, which means there are 3 different axes. You must be familiar with 2 axes which are the x-axis and y-axis but the third axis is known as the z-axis.
Imagine a 2-dimensional space, it has no limit, but you can draw any kind of line on it. That space is known as the plane. The beauty of the plane is that it has no thickness. This means that in 3-dimensional space, there will be infinite planes but how are these planes interconnected? They are interconnected by the z-axis and that is how the z-axis was born.
Imagine two planes and they both have lines on it. Here is how you will represent lines on different planes:
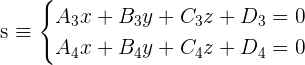
Let's form a system of 2 different planes, here is how you will represent both of them as a single system:
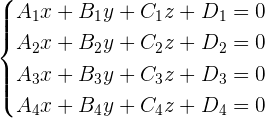
We can calculate the ranks of the above system. With the help of the rank of augmented matrix and coefficient matrix, we can find what kind of relation of lines we are dealing with. Pretty simple, right? If you don't know the representation of augmented matrix and coefficient matrix then here are their representations:
= rank of the coefficient matrix.
= rank of the augmented matrix.
Below are the relationships between the two lines:
Skew Lines
Imagine two or more lines that are neither parallel nor intersecting, we call them agonic lines. However, if we are talking about lines in other planes that are not intersections as well as not parallel, that means they are skew lines. The unique part of skew lines is that they only exist in three or more dimensions.
If 
, that indicates the lines are skew lines. For example, check both lines in the below planes. The above line's rank is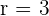 
and the augmented matrix rank is 
. That means both lines are skew lines.
Intersecting Lines
The basic condition for the intersecting line is that both lines should cut each other on a single point.
The identification of intersecting lines is that the rank of the matrix will always be equal to the rank of the augmented matrix and they both should be equal to 3 i.e.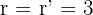 
. For example, in the below plane diagram, the rank of the augmented matrix, as well as the rank of the coefficient matrix, is 3 which means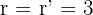
Parallel Lines
Parallel lines mean both lines have a constant distance and they don't meet. Draw a line of 
and draw another line of 
, these vertical lines will never meet each other but lines are identical to each other, except they are at a distance. This distance will remain constant. The rank of the parallel line will always be equal to 
, however, the rank of the augmented matrix will always be equal to 
i.e. 
.
Coincident Lines
Imagine a line and then draw another line which is overlapping the first line. In this case, at every point, there will be an intersecting point. The result will be that there will be an infinite number of intersection points, therefore, we will say that there will be an infinite number of intersecting points.
At this point, you might be wondering what is the difference between intersecting lines and coincident lines, the only difference is that the intersecting line will always intersect at a single point, however, coincident lines intersect at many points that we make it equal to infinity. Furthermore, the coefficient rank of coincident lines will be 
and the rank of the augmented matrix will be equal to 
i.e.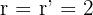 
Q. State the relationship between the following lines:
Example 1
Form a system of equations:
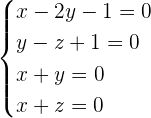
Find the rank of the coefficient matrix.
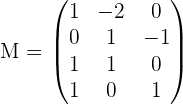
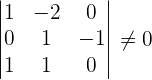
Determine the rank of the augmented matrix.
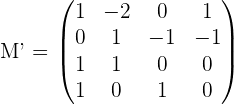
Compare the ranks
They are skew lines.
Example 2.
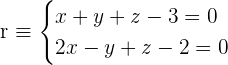
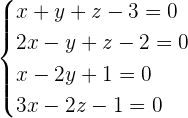
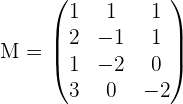
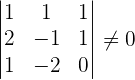
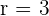
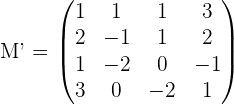
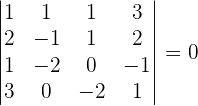
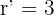
They are intersecting lines.
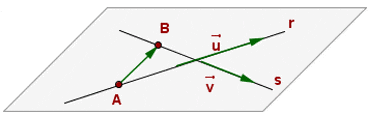
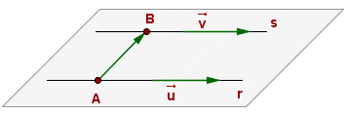
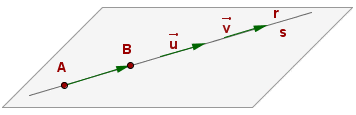
Lines Defined by a Point and a Vector
If the line, r, is determined by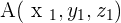 
and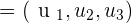 
, and the line, s, is determined by 
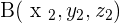and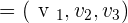 
, the intersection of r and s is given by the position of 
.
If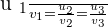 
, there are two possibilities:
1. Conincident lines if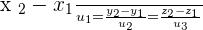 
2. Parallel lines if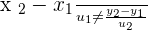 
or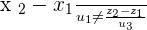 
If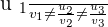 
, there are two other possibilities:
3. Intersecting lines if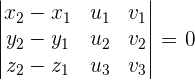 
4. Skew lines if 
Did you like this article? Rate it!
Loading...
