Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
Exercise 1
Determine the equations of the coordinate axes and the coordinate planes.
Exercise 2
Determine the equation of the plane that contains the lines:
Exercise 3
Determine the equation of the plane that contains the point A = (2, 5, 1) and the line:
Exercise 4
Find the intersecting point between the plane x + 2y − z − 2 = 0, the line determined by the point (1, −3, 2) and the vector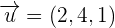 
.
Exercise 5
Determine, in intercept form, the equation of the plane that passes through the points A = (2, 0, 0), B = (0, 4, 0) and C = (0, 0, 7).
Exercise 6
π is a plane that passes through P = (1, 2, 1) and intersects the positive coordinate semi-axes at points A, B and C. If ABC is an equilateral triangle, determine the equations of π.
Exercise 7
Find the equation of the plane that passes through the point P = (1, 1, 1) and is parallel to:
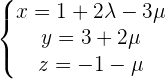
Exercise 8
Determine the equation of the plane that contains the line 
and is parallel to the line 
.
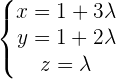Exercise 9
Calculate the equation of the plane that passes through the point (1, 1, 2) and is parallel to the following lines:
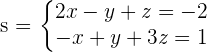
Solution of exercise 1
Determine the equations of the coordinate axes and the coordinate planes.
x - axis O = (0, 0, 0)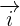 
= (1, 0, 0)
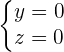
y - axis O = (0, 0, 0) 
(0, 1, 0)
z - axis O (0, 0, 0)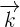 
= (0, 0, 1)
XOY O = (0, 0, 0) 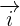= (1, 0, 0) = (0, 1, 0)
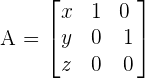
z = 0
XOZ 0 = (0, 0, 0) = (1, 0, 0) 
= (0, 0, 1)
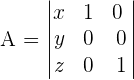
y = 0
YOZ O = (0, 0, 0) = (0, 1, 0) = (0, 0, 1)
x = 0
Solution of exercise 2
Determine the equation of the plane that contains the lines:
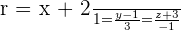
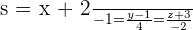
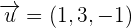
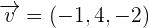
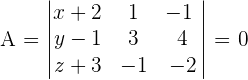
-2x + 3y + 7z + 14 = 0
Solution of exercise 3
Determine the equation of the plane that contains the point A = (2, 5, 1) and the line:
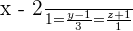
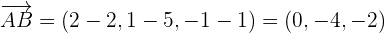
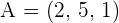
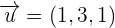
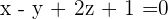
Solution of exercise 4
Find the intersecting point between the plane x + 2y − z − 2 = 0, the line determined by the point (1, −3, 2) and the vector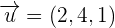 
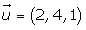
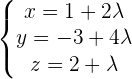
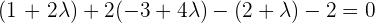
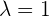
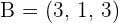
Solution of exercise 5
Determine, in intercept form, the equation of the plane that passes through the points A = (2, 0, 0), B = (0, 4, 0) and C = (0, 0, 7).
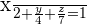
Solution of exercise 6
π is a plane that passes through P = (1, 2, 1) and intersects the positive coordinate semi-axes at points A, B and C. If ABC is an equilateral triangle, determine the equations of π.
A = (a, 0, 0) B = (0, b, 0) C = (0, 0, c)
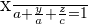
As the triangle is equilateral, the three line segments are equal.
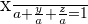
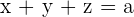
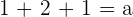
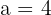
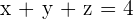
Solution of exercise 7
Find the equation of the plane that passes through the point P = (1, 1, 1) and is parallel to:
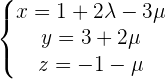
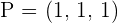
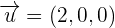
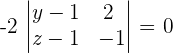
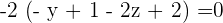
Solution of exercise 8
Determine the equation of the plane that contains the line and is parallel to the line .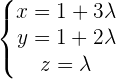
The point A = (2, 2, 4) and the vector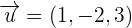 
belong to the plane because the line is in the plane.
The vector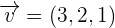 
is a vector in the plane because it is parallel to the line.
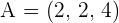
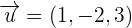
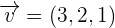
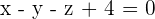
Solution of exercise 9
Calculate the equation of the plane that passes through the point (1, 1, 2) and is parallel to the following lines:
Did you like this article? Rate it!
Loading...
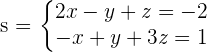
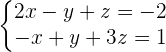
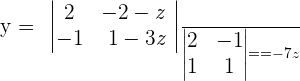
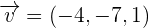
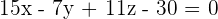
I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html