Chapters
At this point, you have a clear concept of what are planes and vectors. Plane do have equations of their own but how these equations are constructed? That is the real question here. These equations are formed using the primary coordinates and vectors. These vectors are drawn from the coordinates to these planes and with the help of vectors, we came up with plane equations.

Vector Equation of the Plane
To determine the equation of a plane in 3D space, a point P and a pair of vectors that form a basis (linearly independent vectors) must be known.
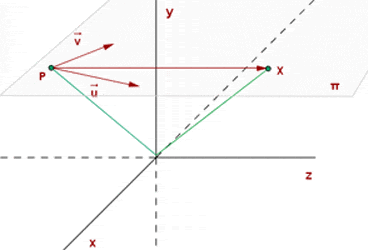
The point P belongs to the plane 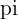 if the vector
if the vector 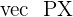 is coplanar with the vectors
is coplanar with the vectors  and
and 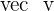 .
.
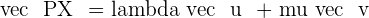
However, the vector 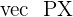 is also formed by two vectors from x,y, and z coordinates. This vector is formed from the vector
is also formed by two vectors from x,y, and z coordinates. This vector is formed from the vector 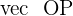 and
and  .
.

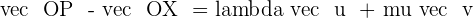
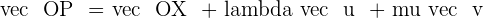
Let's check the coordinate form.
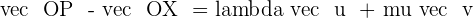

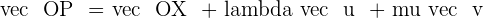

Parametric Equations of the Plane
To solve these vectors, we will need to make parametric equations. These parametric equations can be solved easily using the matrix method, which we will teach you in upcoming headings.

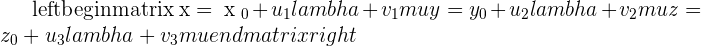
Cartesian Equation of the Plane
A point is in the plane 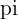 if the system has the solution:
if the system has the solution:

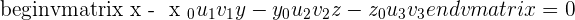
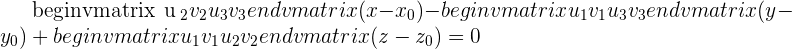
The values are given as:

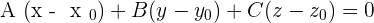
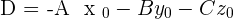
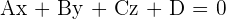
Intercept Form

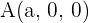 ,
, 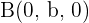 and
and  .
.
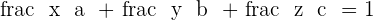
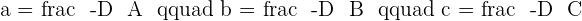
Examples
1.Find the equations of the plane that pass through point  and their direction vectors are:
and their direction vectors are: 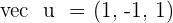 and
and 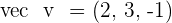 .
.
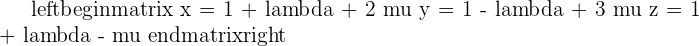
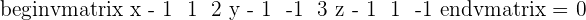
2.Find the equations of the plane that pass through points 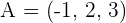 and
and  and contains the vector
and contains the vector  .
.
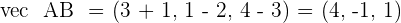
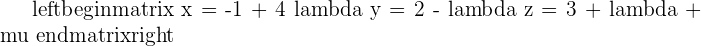
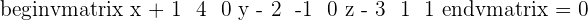
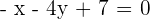
3.Find the equations of the plane that pass through points  ,
, 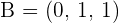 and
and 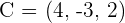 .
.

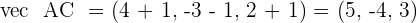
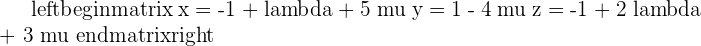
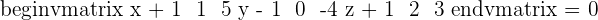
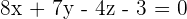
4. π is the plane of parametric equations:

Confirm whether the points 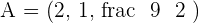 and
and  belong to this plane.
belong to this plane.
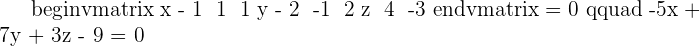
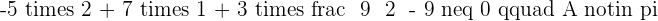
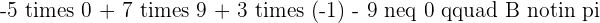
5.Find the equation of the plane in intercept form that passes through the points 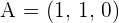 ,
, 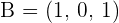 and
and 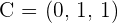 .
.
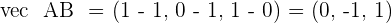
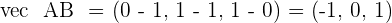
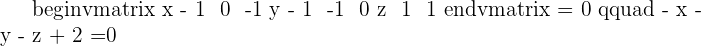
Divide by  , and the equation is obtained:
, and the equation is obtained:

6.Find the equation of the plane that passes through a point 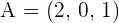 and contains the line with the equation:
and contains the line with the equation:
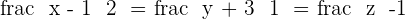
From the equation of the line, a second point and the vector  is obtained.
is obtained.
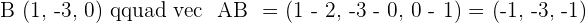
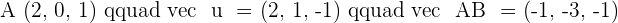
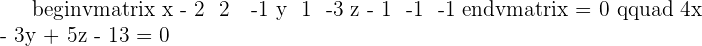
7.Find the equation of the plane that passes through the points 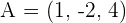 and
and 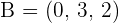 and is parallel to the line:
and is parallel to the line:
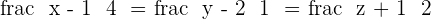
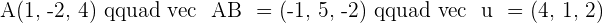
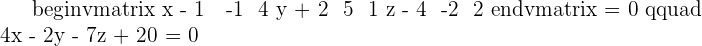
8.Given the lines:
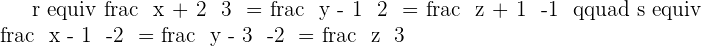
Determine the equation of the plane that contains the line r and is parallel to the line s.

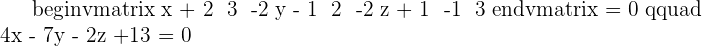












I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html