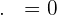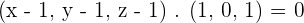Chapters
When any quantity not only depends on its magnitude but also on the direction as well, we will call it a vector. A vector has two things, one is the magnitude and the other is direction. There are different types of vectors such as parallel vectors, perpendicular vectors, but here, we will discuss normal vectors. Imagine two vectors, one of them is drawn on the plane. The other vector is drawn on the tail of the first vector and the direction is perpendicular to the plane, this type of vector is called a normal vector. Consider the below example:
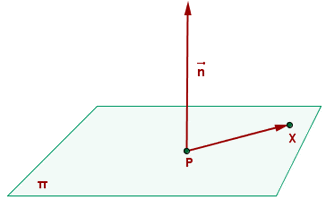
In the above example, the vector 
is perpendicular to the plane. When we are talking about normal vectors, we don't consider the plane but we do consider if the vector is perpendicular to any other vector? So, if you check the example again, the vector 
is perpendicular to the vector 
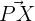. In short, the vector 
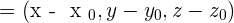is perpendicular to the vector .
How to identify if two vectors are normal? The best way to find that is through the dot product of both vectors. Below is the formula of dot product:
where 
is the angle between two vectors
In the case of the normal vector, the angle between both angles will be equal to 
°. We all know that the 
, let's put this zero in the dot product formula:
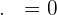
This concludes that if try to find the dot product of a normal vector, you will always get zero and that is the identity of a normal vector. That is why the equation of the plane can be determined from a point and a normal vector. At this point you might be confused that what is a difference between normal vector and perpendicular vector? The answer is there is almost no difference. They have minor difference and these different aroses in different programming languages or simulations. However, in mathematical world, they don't have any difference, both means the same.
Examples
1. Find the equation of the line 
, that passes through the point 
and is perpendicular to the plane 
.
Plane = 
A =
2. Find the equation of the plane, 
, that passes through the point 
and is perpendicular to the lines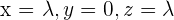 
.
As the plane and the line are perpendicular to each other, the direction vector of the line is a normal vector of the plane.
Did you like this article? Rate it!
Loading...
