Chapters

What is a Line
Lines in space sounds like a complex topic. Let’s break it down to its most basic unit: a line. When we talk about lines, it is usually easier to put that line on a graph. A graph usually looks like the following.

This is what we know as a Cartesian plane. A cartesian plane always has the same properties, which you can see highlighted above.
| Property 1 | Four quadrants going counter-clockwise |
| Property 2 | Two axes: the x-axis and y-axis |
| Property 3 | The two axes form a right triangle |
| Property 4 | There are only two directions corresponding to each axis |
When we draw a line on a graph, we only need two things: two points. In fact, any two points can form a line, no matter how close or far apart they are.
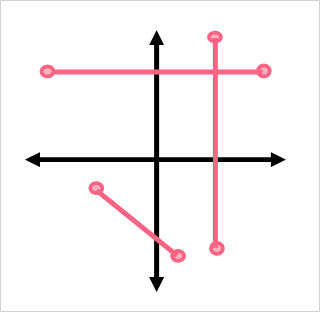
A Line in Two Dimensions
The cartesian plane is an example of two dimensions. While two dimensional geometry sounds a bit complex, it’s actually quite simple. It will make more sense with the definition of a 2 dimensional plane.
| Definition | Example | |
| Two-Dimensional | A space that only has two directions | Cartesian plane |
A line in two dimensional space is simply any line on a cartesian plane. This is where the idea of quadrants really comes in handy. When you have any coordinate on a cartesian plane, you can locate them by going in only two directions.
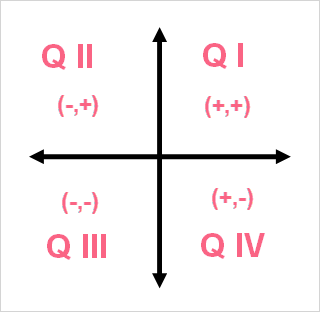
| Quadrant 1 | (+,+) | (right, up) |
| Quadrant 2 | (-,+) | (left, up) |
| Quadrant 3 | (-,-) | (left, down) |
| Quadrant 4 | (+,-) | (right, down) |
As you can see, in any given quadrant, you can only go in two directions to locate a coordinate. A line can be thought of as two points, but you can also think about the infinite amount of points that you can fit in between those two points.

In this way, a line is simply a collection of points.
The 3 Equations of a Line
When you have a line in two-dimensional plane, you actually have three different formulas you can work with. Take a look at them below.

| Standard From | Slope-Intercept | Point-Slope Formula |
 |  |  |
| -3x + 7y = 14 | y= x+2 x+2 | y-5 =  * (x - 7) * (x - 7) |
As you can see, we can write the same line three different ways. Let’s break down each formula and what they mean.
Slope Intercept
The slope intercept form is the simplest of the three. This is because it is the most common. Let’s break it down to its elements.
| y | The y value that the formula gives when we plug in the x coordinate. We can also rearrange the formula so it gives us the x-value for any y-value:  |
| x | The x value that we can plug in. This is the x coordinate. |
| m | The slope of the line. This slope tells us how sharp or subtle the incline or decline is. |
| b | The y-intercept, which is the value of the y coordinate where the line crosses the y-axis. In other words, the point where the x coordinate is zero. |
In order to find the slope, you simply need to find the rise over the run. In other words, the vertical length of two points divided by the horizontal length of the two points.
| Point 1 |  |
| Point 2 | 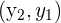 |
| The vertical length | 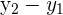 |
| The horizontal length | 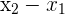 |
| The slope |  |
Standard Form
In order to understand the standard form, let’s see how we get to the standard form from the slope-intercept form. Keep in mind that one line can be written in any of the three ways we presented. Let’s take our example form earlier.
\[
y = \frac{3}{7}x+2
\]
In the standard form, the x and y values are on the same side. So, what we need to do is try to get rid of the fraction.
| Step 1 | Get rid of the fraction |  |
| Step 2 | Simplify | 7y = 3x + 14 |
| Step 3 | Get x and y to the same side | 7y - 3x = 14 |
| Step 4 | Arrange into standard form | -3x + 7y = 14 |
As you can see, we can derive the standard form from the slope-intercept formula. Now, let’s discuss what these components mean. Remember that the standard form is the following.
\[
Ax+By=C
\]
Let’s take a look at each value:
| A | B | C |
| -3 | 7 | 14 |
In order to find the x and y intercept, you should follow these rules.
| Rule | Example | |
| x-intercept |  |  = -4.67 = -4.67 |
| y-intercept |  |  = 2 = 2 |
Point-Slope Formula
The last formula is the point-slope formula. Typically, when we have the slope-intercept form, we have to know these two things:
| Known 1 | Slope |
| Known 2 | y-intercept |
However, we often have to find the y-intercept in order to use the formula. This is the scenario where the point-slope formula is most useful. For the point-slope formula, we only need these two things.
| Known 1 | Slope |
| Known 2 | A point |
Let’s take our example again, only this time, let’s say that you only know the slope and a point.
| Known 1 | Slope |  |
| Known 2 | A point | (7,5) |
Given these, we don’t need to plug in the point to find the y-intercept and then be able to use the equation. Instead, we can use the point-slope formula directly.
| Step 1 | Get the point slope formula |  |
| Step 2 | Replace the slope and the point into the formula |  |
Just like that, we have a simple equation for the line. We can go further and turn the point slope formula into the slope-intercept formula.
| Step 1 | Start with point-slope form |  |
| Step 2 | Multiply the slope to both numbers |  |
| Step 3 | Get the y by itself |  |
| Step 4 | Simplify |  |
As you can see, this is exactly like our original slope-intercept formula.













