Chapters

Types of Triangles
| Definition | |
| Triangle | A polygon that has three sides, whose corners form three angles |
No matter what type of triangle you have, there are certain properties that all triangles have. Take a look at the most important property below.
| Description | |
| Angle Sum Property | All 3 interior angles have a sum of 180 degrees |
The three types of triangles and their properties can be found below.
| Equilateral Triangle | Has three equal sides and three equal angles | Acute |
| Isosceles Triangle | Has two equal sides and two equal angles | Right, obtuse or acute |
| Scalene Triangle | Has no equal sides and no equal angles | Right, obtuse or acute |
Perimeter of a Triangle
The perimeter can be found for any shape. The definition of a perimeter and its notation can be found below.
| Definition | Notation | |
| Perimeter | The sum of each side of the shape |  |
The perimeter of a triangle depends on what type of triangle you’re dealing with. Take a look at the formulas below.

| A | B | C | |
| Triangle | Equilateral | Isosceles | Scalene |
| Perimeter Formula |  |  |  |
Shapes have special notation for sides that are of equal length, which is called congruent. Congruent sides are marked by dashes of the same number. Take a look at the example below.
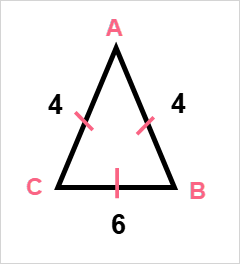
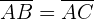 |  |
| 4 = 4 | 6 |
Area of a Triangle
The area of any shape can be defined as the number of base units that can be contained inside of that shape’s boundary. Take a look at the example below.

| Base Unit | Notation of Area | Definition | Example |
| 1 square |  | How many unit squares fit inside | 4 unit squares |
The area of a triangle can be found in a variety of ways. In general, there are two equations you can use to find the area of a triangle, depending on the type of triangle you have.
| Type | Area Formula |
| Any triangle |  |
| Equilateral triangle |  |
The notation of the variables in the formulas above can be explained by the following image.

 |  |  |
| Any side | Base of the triangle | Height of the triangle |
Pythagorean Theorem
The Pythagorean theorem is one of the most important theorems of mathematics. The definition of the theorem can be seen in the table below.
| Pythagorean Theorem | |
| When can it be used? | When you have any right triangle |
| What does it say? | The sum of the square of the lengths of the two smaller sides equal the square of the longer side |
| What is the formula? |  |
| Why is it important? | You can find the length of any side of a right triangle if you have the lengths of the other two sides |
Problem 1
Find the perimeter of an equilateral triangle given the following information.
 | |
| Equilateral Triangle | 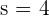 |
Problem 2
Find the perimeter of the triangle formed by the diagonal of the following square.
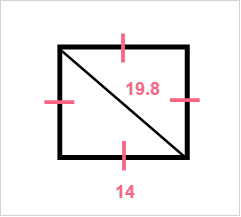
Problem 3
Find the area of the following triangle.

Problem 4
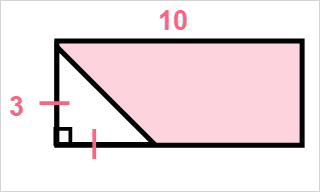
Find the perimeter of the shaded region.
Solution 1
Here, because we have an equilateral triangle, we know that all the sides are equal to each other. Since we have the length of one side, we can easily find the parameter.
 |  | |
| Equilateral Triangle | 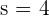 | 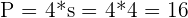 |
Solution 2
Here, we have to find the perimeter of the triangle formed by the diagonal of the square. Here, we have to use the properties of a square.
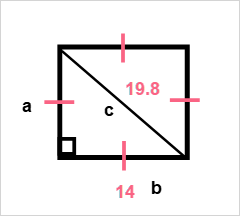
Since a square is made of four right angles, the triangle formed by the diagonal is a right angle. Here, we can use the Pythagorean theorem to find the perimeter.
| Step 1 | Use the formula of the Pythagorean theorem |  |
| Step 2 | Rearrange to find b | 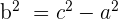 |
| Step 3 | Solve for b | 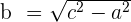 |
| Step 4 | Plug in the numbers | 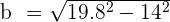
|
| Step b | Add the sides to get the perimeter |  |
Solution 3
In order to find the area of the equilateral triangle, you should keep the properties of the equilateral triangle in mind.
| Property 1 | All sides are the same length |
| Property 2 | The height bisects the base with the midpoint that is halfway between the whole base |
This translates into the following.
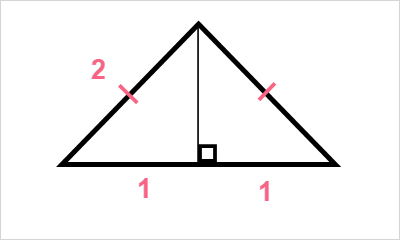
| Step 1 | Use the formula of the Pythagorean theorem |  |
| Step 2 | Rearrange to find a | 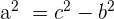 |
| Step 3 | Solve for a | 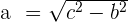 |
| Step 4 | Plug in the numbers | 
|
| Step 5 | Use the area formula |  |
Solution 4
Here, we have to find the perimeter of the shaded region. Follow the following steps.
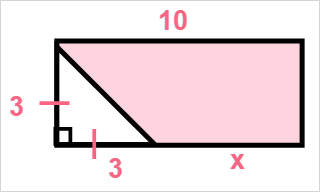
| Step 1 | Find the length of the hypotenuse by using the Pythagorean theorem | 
|
| Step 2 | Solve for C | 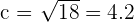 |
| Step 3 | Find the length of x | 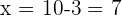 |
| Step 4 | Find the perimeter of the shaded area | 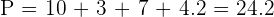 |














I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html