Chapters

Exercise 1
Given an equilateral triangle with a side of 6 cm, find the area of the circular sector determined by the circle circumscribed around the triangle and the radius passing through the vertices.
Exercise 2
Calculate the area enclosed by the inscribed and circumscribed circles to a square with a diagonal of 8 m in length.
Exercise 3
If non-parallel sides of an isosceles trapezoid are prolonged, an equilateral triangle with sides of 6 cm would be formed. Knowing that the trapezoid is half the height of the triangle, calculate the area of the trapezoid.
Exercise 4
The area of a square is 2,304 cm². Calculate the area of a regular hexagon that has the same perimeter as this square.
Exercise 5
A square is inscribed in a circle of 4 m radius and on the sides of the square are outward pointing equilateral triangles. Calculate the area of this shape.
Solution of exercise 1
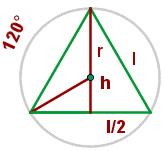
Given an equilateral triangle with a side of 6 cm, find the area of the circular sector determined by the circle circumscribed around the triangle and the radius passing through the vertices.
The centre of the circle is the centroid. Therefore:
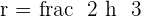
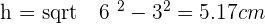


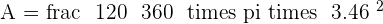

Solution of exercise 2
Calculate the area enclosed by the inscribed and circumscribed circles to a square with a diagonal of 8 m in length.

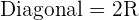
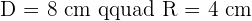

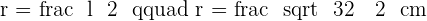

Solution of exercise 3
If non-parallel sides of an isosceles trapezoid are prolonged, an equilateral triangle with sides of 6 cm would be formed. Knowing that the trapezoid is half the height of the triangle, calculate the area of the trapezoid.
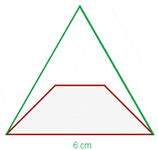
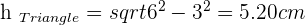
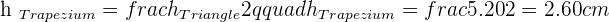
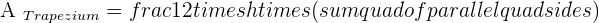
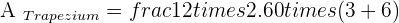
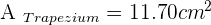
Solution of exercise 4
The area of a square is 2,304 cm². Calculate the area of a regular hexagon that has the same perimeter as this square.
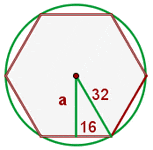
Area of square = 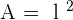

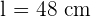


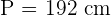



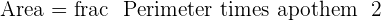

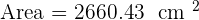
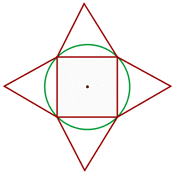
Solution of exercise 5
A square is inscribed in a circle of 4 m radius and on the sides of the square are outward pointing equilateral triangles. Calculate the area of this shape.

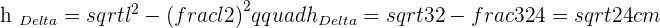














I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html