Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10

Exercise 1
A 10 m long ladder is leaning against a wall. The bottom of the ladder is 6 m from the base of where the wall meets the ground. At what height from the ground does the top of the ladder lean against the wall?
Exercise 2
Determine the side of an equilateral triangle whose perimeter is equal to a square of side 12 cm. Are their areas equal?
Exercise 3
Calculate the area of an equilateral triangle inscribed in a circle of radius 6 cm.
Exercise 4
Determine the area of the square inscribed in a circle with a circumference of 18.84 cm.
Exercise 5
A square with a side of 2 m has a circle inscribed in it and in turn this circle has a square inscribed in it. If this square also has a circle inscribed in it, what is the area between the last square and the last circle.
Exercise 6
The perimeter of an isosceles trapezoid is 110 m and the bases are 40 and 30 m in length. Calculate the length of the non-parallel sides of the trapezoid and its area.
Exercise 7
A regular hexagon of side 4 cm has a circle inscribed and another circumscribed around its shape. Find the area enclosed between these two concentric circles.
Exercise 8
A chord of 48 cm is 7 cm from the center of a circle. Calculate the area of the circle.
Exercise 9
The legs of a right triangle inscribed in a circle measure 22.2 cm and 29.6 cm. Calculate the circumference and the area of the circle.
Exercise 10
A central angle of 60° is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment between the chord joining the ends of the two radii and its corresponding arc.
Solution of exercise 1
A 10 m long ladder is leaning against a wall. The bottom of the ladder is 6 m from the base of where the wall meets the ground. At what height from the ground does the top of the ladder lean against the wall?

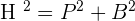


Solution of exercise 2
Determine the side of an equilateral triangle whose perimeter is equal to a square of side 12 cm. Are their areas equal?










Solution of exercise 3
Calculate the area of an equilateral triangle inscribed in a circle of radius 6 cm.
The centre of the circle is the centroid. Therefore:




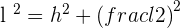



Solution of exercise 4
Determine the area of the square inscribed in a circle with a circumference of 18.84 cm.






Solution of exercise 5
A square with a side of 2 m has a circle inscribed in it and in turn this circle has a square inscribed in it. If this square also has a circle inscribed in it, what is the area between the last square and the last circle.


Diameter = Diagonal of the second square






Solution of exercise 6
The perimeter of an isosceles trapezoid is 110 m and the bases are 40 and 30 m in length. Calculate the length of the non-parallel sides of the trapezoid and its area.


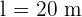



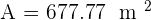
Solution of exercise 7
A regular hexagon of a side 4 cm has a circle inscribed and another circumscribed around its shape. Find the area enclosed between these two concentric circles.




Solution of exercise 8
A chord of 48 cm is 7 cm from the center of a circle. Calculate the area of the circle.





Solution of exercise 9
The legs of a right triangle inscribed in a circle measure 22.2 cm and 29.6 cm. Calculate the circumference and the area of the circle.
A triangle inscribed whose diameter coincides with the hypotenuse is always a right triangle.




Solution of exercise 10
A central angle of 60° is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment between the chord joining the ends of the two radii and its corresponding arc.


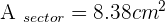



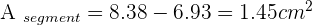












I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html