In this article, we will discuss inscribed polygons in detail. But before proceeding to discuss inscribed polygons, first, let us recall what are polygons, their types, and their properties.

What is a Polygon?
The word polygon is created by combining two words: Poly and gon. Poly means many and gon means sides. It means that a polygon is a geometrical figure that has multiple sides. The sides of the polygons are straight line segments that are joined end to end with each other. These sides are also referred to as edges of the polygon. Vertex of the polygon refers to a point where two line segments meet each other. At the vertex, the angle of the polygon is also formed.
Some examples of polygons include triangle, square, rectangle, rhombus, and hexagon. All these figures are two-dimensional. A circle is also a two-dimensional figure, but it is not a polygon because it does not have angles or sides, rather it is a simple curved figure.
Types of Polygon
A polygon is divided into four different categories based on its angles and sides. These types are:
- Regular Polygon: All sides and interior angles of a regular polygon are equal
- Irregular Polygon: All sides and interior angles of an irregular polygon are not equal
- Convex Polygon: All the interior angles of the convex polygon are strictly less than 180 degrees.
- Concave polygon: One or more interior angles of a concave polygon are greater than 180 degrees
Properties of Polygon
Just like the types of polygon, the properties of polygons are also based on their sides and angles. In this section, we have listed down some of the properties of polygons.
- In an n-sided polygon, the sum of all the interior angles is equal to
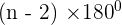
- The number of diagonals in a polygon having "n" number of sides is equal to

- In an n-sided polygon, the measure of each interior angle is equal to

- The number of triangles created by connecting the diagonals from one corner of a polygon can be calculated using the expression (n - 2)
- Each exterior angle of an n-sided polygon is equal to
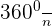
Now, in the next section, we will discuss what is an inscribed polygon in detail.
Inscribed Polygon
A polygon is inscribed in a circle if all its vertices are points on the circle and all sides are included within the circle. A polygon inscribed within a circle is also referred to as a cyclic polygon. Consider the figure below in which a regular pentagon is inscribed in a circle.

Remember that:
- All regular polygons can be inscribed in a circle.
- The center of an inscribed polygon is also the center of the circumscribed circle.
- The radius of the inscribed polygon is also the radius of the circumscribed circle.
In the next section, we will see how to calculate certain parameters of the polygons inscribed within a circle.
Side of an Inscribed Square
A square is a regular polygon in which all sides and angles are of the same measure. The following figure shows the square that is inscribed within a circle.
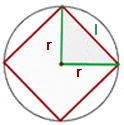
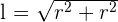
Example
Find the side of a square inscribed in a circle of 5 cm radius.

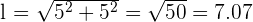 cm
cmApothem of an Inscribed Hexagon
Now, we will see how to calculate the apothem of the inscribed hexagon. Before calculating apothem, first, let us recall what is apothem.
Apothem refers to the distance between the midpoint of any of the sides of the hexagon and the center
It can be considered as the height of an equilateral triangle created by taking one side and two radii of the hexagon.
In the figure below, you can see that length of the side of a hexagon is equal to the radius of the circle. Hence, we can say that:
l = r
We can make a triangle as shown below by using the radius of the circle. The base of the triangle will be equal to half of the side of a triangle.


Example
Calculate the apothem of a hexagon inscribed in a circle of 4 cm radius.
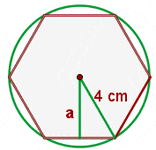

Side of an Equilateral Triangle Inscribed in a Circle
Consider the following figure in which an equilateral triangle is inscribed within a circle.
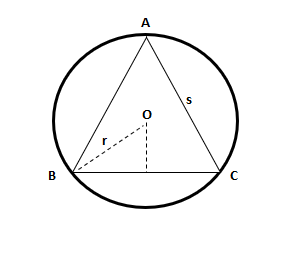
All the sides and angles of an equilateral triangle are equal. In the above equilateral triangle, the length of the side of the triangle is equal to "s". The following formula is used to calculate the side length of the triangle:

Example
An equilateral triangle is inscribed within a circle whose area is  . Find the length of the side of the triangle.
. Find the length of the side of the triangle.
Solution
To calculate the length of the side of a triangle, we need to know the radius of the circle. In this example, we are not given the radius. From the given area, we can easily find the radius of the circle.
Area of the circle = 
 =
= 

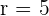
Now, we know the radius of the circle, we can easily calculate the length of the side of the equilateral triangle using the following formula:
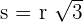
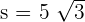
So, the length of the side of the triangle is 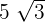 cm.
cm.













I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html