Chapters
What is a Circle
Circles are one of the most important shapes in math. We are surrounded by appliances, entertainment and ideas that use circles at their base. Let’s take a look at the definition of a circle.
| Definition | Notation | |
| Circle | A line that follows the shape of a loop where every point on that line is equidistant from a centre point |  |
Circles, no matter what their size, always have the same properties. Let’s take a look at those properties.
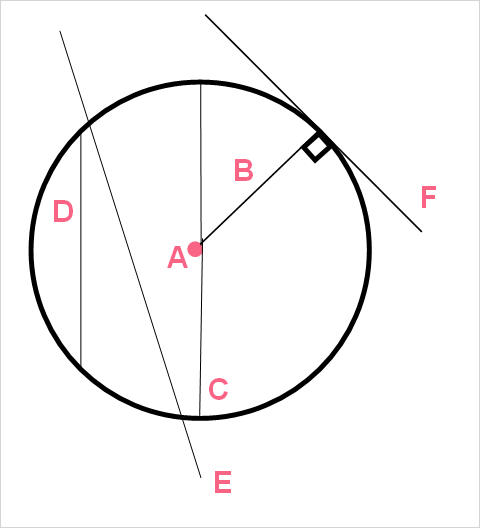
| A | centre point | The point at the centre of the circle |
| B | Radius | The distance from the centre point to any point on the circle |
| C | Diameter | The distance across the circle that passes through the centre point |
| D | Chord | A line segment that connects any two points on the circle line |
| E | Secant | A line that intersects the circle at any two points |
| F | Tangent | A line that touches the circle line at a 90 degree angle |
Perimeter of a Circle
The perimeter of a circle is defined below, as well as the notation most commonly used for the perimeter of a circle.
| Name | Definition | Notation | |
| Perimeter | Circumference | The distance around the circle |  |
There are three different ways to find the circumference, or the perimeter of a circle. Take a look at the table below to see the different formulas.
| Formula | |
| Using the radius |  |
| Using the diameter |  |
| Using the area |  |
There are some useful formulas you should keep in mind about the properties of circles as well. Take a look below.
| Parameter | Circumference | Area | |
| Diameter |  |  |  |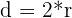
| Radius |  |  |  |
Area of a Circle
The area of a circle is the size of the space contained within the boundary of the circle. You can also think of the area as the size of the space inside of the perimeter. There are several different ways you can find the entire area of the circle depending on what information you have about that circle.
Take a look at the following formulas, which will all give you the area of a circle.
| You have the radius |  |  |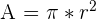
| You have the diameter |  |  |
| You have the circumference | |  |
Circular Sector Area
While you may have heard of circles your entire life, chances are you’ve rarely heard of circle sectors. While circle sectors are less common in day to day life, they’re an extremely important idea in many different disciplines.
A circular sector is defined as the region of a circle that is formed between two radii (that’s the plural of radius) and the arc on the circle between them. Just imagine a pizza slice that is perfectly cut from the centre point of the pizza.
To find the area of a circle sector, you can simply use the angle that the two radii form, the length of the radius and pie.
\[
A = \frac{\theta}{360^{o}} \; * \pie * r^{2}
\]
Area Between Two Concentric Circles
Concentric circle is another term that you probably haven’t heard much about before. However, you may have heard the word concentric before. If you think about the ripples that a drop of water makes, you will have an idea of what concentric circles are.
Concentric circles are defined as circles that share the same centre point. In order to be concentric, they must also be on the same plane. Concentric circles don’t have the same radius, which means that concentric circles contain or surround one another.
The area of the region between two concentric circles can be found with the following formula.
\[
A = \pi(R^{2} - r^{2})
\]
Where R is the radius of the bigger circle.
Problem 1
Given the following parameters, find the area and perimeter of the circle.
| r | 4 |
| C | 50.265 |
Problem 2
A circle has the following circumference. Given this information, find the area of the circle.
\[
C = 28.274
\]
Problem 3
You are given the following properties of the circle below. Given this information, calculate the area of the circle sector.
| Radius | 4 |
 (angle of sector) | 45 |
Problem 4
Find the area of the shaded region given the following parameters.
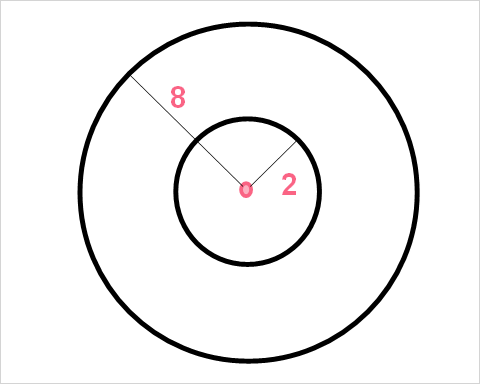
| Diameter of bigger circle | 8 |
| Diameter of smaller circle | 2 |
Problem 5
Find the area in the shaded region given that the following information.
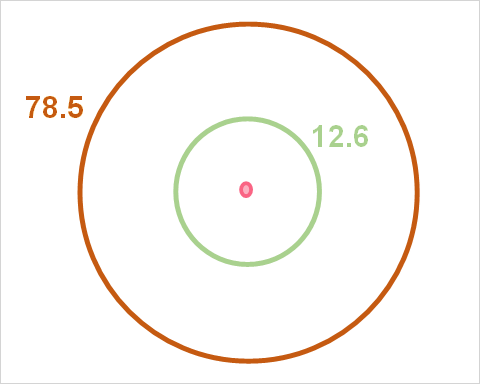
| C of bigger circle | 78.5398 |
| C of smaller circle | 12.5664 |
Solution Problem 1
Remember that the perimeter of a circle is denoted as C, the circumference. So C = 50.265.
This is how you find the area.
\[
A = \pi * 4^{2} = 50.3
\]
Solution Problem 2
You can find the area using the circumference.
\[
A = \frac{(28.274)^{2}}{4* \pi} = 63.6
\]
Problem 3
Plug the radii into the formula:
\[
A = \frac{45^{o}}{360^{o}}*\pi * 4^{2} = 6.28
\]
Problem 4
The radius is just half of the diameter, so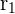 
= 8/2 = 4 and 
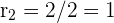. Plug these into the formula.
\[
A = \pi(4^{2} - 1^{2}) = 47.12
\]
Problem 5
To find the area, solve for the area of both circles.
\[
A = \frac{(78.5398)^{2}}{4* \pi} = 491
\]
\[
A = \frac{(12.5664)^{2}}{4* \pi} = 13
\]
The shaded region is the bigger - smaller circle: 491-13 = 478.
Did you like this article? Rate it!
Loading...
I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html