Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10

Exercise 1
Anne is riding a horse which is tied to a pole with a 3.5 m piece of rope and her friend Laura is riding a donkey which is 2 m from the same center point. Calculate the distance travelled by each when they have rotated 50 times around the centre.
Exercise 2
The rope that attaches a swing to a tree is 1.8 m long and the maximum difference between trajectories is an angle of 146°. Calculate the maximum distance travelled by the seat of the swing when the swing angle is described as the maximum.
Exercise 3
Find the area of a circular sector whose chord is the side of the square inscribed in a circle with a 4 cm radius.
Exercise 4
Calculate the shaded area, knowing that the side of the outer square is 6 cm and the radius of the circle is 3 cm.

Exercise 5
In a circular park with a radius of 250 m there are 7 lamps whose bases are circles with a radius of 1 m. The entire area of the park has grass with the exception of the bases for the lamps. Calculate the lawn area.
Exercise 6
Two radii (plural for radius) OA and OB form an angle of 60° for two concentric circles with 8 and 5 cm radii. Calculate the area of the circular trapezoid formed by the radii and concentric circles.
Exercise 7
A circular fountain of 5 m radius lies alone in the centre of a circular park of 700 m radius. Calculate the total walking area available to pedestrians visiting the park.
Exercise 8
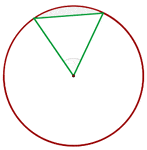
A central angle of 60° is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment between the chord joining the ends of the two radii and its corresponding arc.
Exercise 9
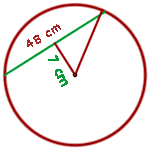
A chord of 48 cm is 7 cm from the center of a circle. Calculate the area of the circle.
Exercise 10
Calculate the area enclosed by the inscribed and circumscribed circles to a square with a diagonal of 8 m in length.
Solution of exercise 1
Anne is riding a horse which is tied to a pole with a 3.5 m piece of rope and her friend Laura is riding a donkey which is 2 m from the same center point. Calculate the distance travelled by each when they have rotated 50 times around the center.
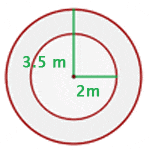
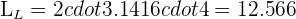 m
m

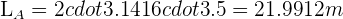

Solution of exercise 2
The rope that attaches a swing to a tree is 1.8 m long and the maximum difference between trajectories is an angle of 146°. Calculate the maximum distance travelled by the seat of the swing when the swing angle is described as the maximum.
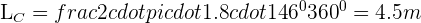
Solution of exercise 3
Find the area of a circular sector whose chord is the side of the square inscribed in a circle with a 4 cm radius.

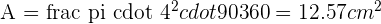
Solution of exercise 4
Calculate the shaded area, knowing that the side of the outer square is 6 cm and the radius of the circle is 3 cm.
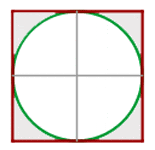
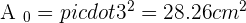
Area of a square = 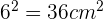
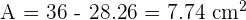
Solution of exercise 5
In a circular park with a radius of 250 m there are 7 lamps whose bases are circles with a radius of 1 m. The entire area of the park has grass with the exception of the bases for the lamps. Calculate the lawn area.


Solution of exercise 6
Two radii (plural for radius) OA and OB form an angle of 60° for two concentric circles with 8 and 5 cm radii. Calculate the area of the circular trapezoid formed by the radii and concentric circles.
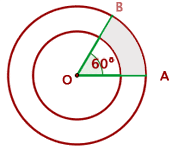
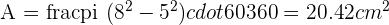
Solution of exercise 7
A circular fountain of 5 m radius lies alone in the center of a circular park of 700 m radius. Calculate the total walking area available to pedestrians visiting the park.

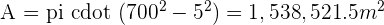
Solution of exercise 8
A central angle of 60° is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment between the chord joining the ends of the two radii and its corresponding arc.


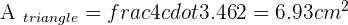
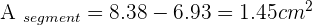
Solution of exercise 9
A chord of 48 cm is 7 cm from the center of a circle. Calculate the area of the circle.
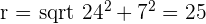
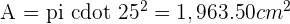
Solution of exercise 10
Calculate the area enclosed by the inscribed and circumscribed circles to a square with a diagonal of 8 m in length.
Diagonal of the square= 2R
D = 8 cm R = 4 cm
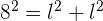
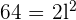

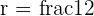

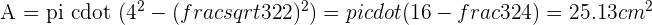













I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html