Chapters

What is an Area
| Area | |
| Definition | The size of the space inside of a shape or boundary |
| Why is it used? | Areas are used in everything from construction to party planning. |
Because we need to be able to compare areas regardless of what shape or boundary we want to find the area for, we use the same basic unit for all areas.
| Definition | Basic Unit | Notation | |
| Area | Size of the space inside a shape or boundary | Unit square |  |
So essentially, when we find the area of a shape or boundary, we’re finding out how many unit squares fit inside of that shape or boundary. Take a look at the examples below.

| A | B | C |
| 1 | 2 | 4 |
In order to understand some of the terms used when describing shapes, you should understand the definitions of some basic concepts.
| Definition | |
| Polygon | A two dimensional shape formed by 3 or more lines |
| Quadrilateral | Any polygon that has four sides |
| Congruent | Two lines that are the same length |
| Parallel | Two lines that never touch and are always the same distance apart |
| Right angle | An angle with 90 degrees |
Area of Rectangle
In order to find the area of a rectangle, let’s first define what a rectangle is. Take a look at the properties of a rectangle below.

| Property 1 | A quadrilateral |
| Property 2 | Has 4 right angles |
| Property 3 | Opposite sides are congruent and parallel |
All of the properties above have special notations. When you have any right angle, you can mark it as below.

| Notation | |
| Right Angle | A small square at the angle |
When we talk about equal sides, or congruent sides, we can also mark them with specific notation. Take a look below.
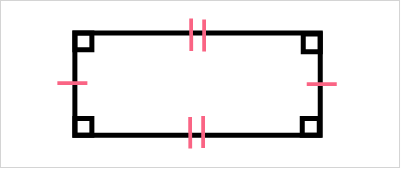
| Notation | |
| Congruent Sides | One dash on the side that matches with another |
As you can see, the opposite sides are marked with matching dashes, meaning they are congruent. Now let’s take a look at the area of a rectangle. In general, shapes have a length and a width. Take a look at the notation below.
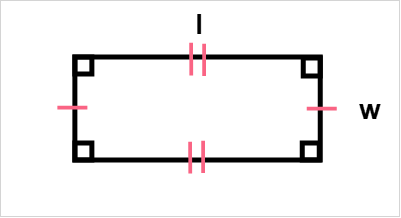
| Notation | |
| Length |  |
| Width |  |
The area formula for a rectangle is written below.
| Area Formula | |
| Rectangle | 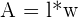 |
Area of Square
To understand the area of a square, let’s first take a look at the properties of a square.
| Property 1 | A quadrilateral |
| Property 2 | Four right angles |
| Property 3 | Four congruent sides |
Now, let’s take a look at the notation of a square.
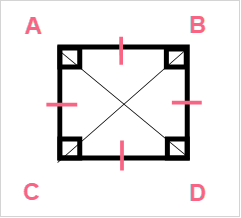
| Four right angles |  |
| Four congruent sides |  |
Because all the sides of a square are of equal length, this means that the length and width of a square are equal to each other. Take a look at the area formula of a square below.
| Sides | Area Formula | |
| Square | 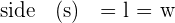 |  |
Area of Circle
Circles are very special shapes in maths. Let’s take a look at the properties of circles in order to better understand how to find the area of a circle.
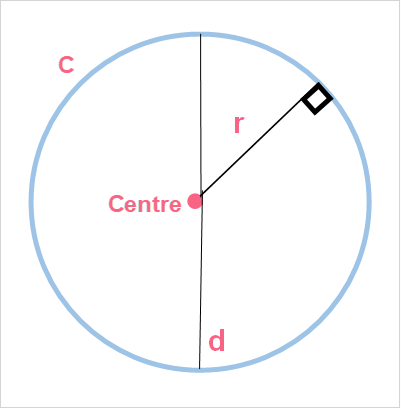
| Property 1 | A circle’s length is called a diameter |  |
| Property 2 | The length from the centre of the circle to the outside is called the radius |  |
| Property 3 | The length around the circle, or the perimeter, is called the circumference |  |
There are three ways you can find the area of a circle using each of the properties above. Take a look at the formulas below.
| Using the diameter |  |
| Using the radius | 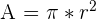 |
| Using the circumference |  |
Area of Equilateral Triangle
While we usually only think of triangles as being the same, there are actually three different types of triangles. These triangles are defined by their properties. Let’s start by looking at an equilateral triangle definition.
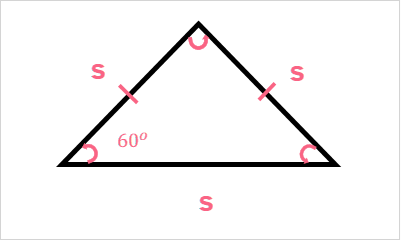
| Definition | |
| Equilateral Triangle | A triangle that has three equal sides and three equal angles, which are all 60 degrees. |
Here, we have a new type of notation we haven’t seen before. This notation is used when we have angles that are the same size. Take a look below.

| Notation | |
| Same angle | Curve at the angle |
The area of an equilateral triangle can be found in the table below.
| Area | |
| Equilateral Triangle |  |
Area of Any Triangle
While you can find the area of an equilateral triangle with the special formula above, the area of triangles can also be found with a general formula. This formula is written below.
| Area Formula | |
| Any triangle |  |
As you can see, this formula uses several variables we haven’t seen before. Take a look at the table below for a description of these variables.

 | Base | The bottom side, or base, of any triangle |
 | Height | The size of the line that goes from the base to the furthest point away from the base. |
Problem 1
Find the area of the circle with the following parameters.
| Diameter | Radius | Circumference |
| 6 | 3 | 18.85 |
Problem 2
Find the area of the shaded region below.

Problem 3
Find the area of the triangle below.

Solution Problem 1
In this problem, you can find the area of the circle three different ways given the parameters.
| Using the diameter |  |  |
| Using the radius | 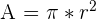 |  |
| Using the circumference |  |  |
The area is equal to 28.27.
Solution Problem 2
Here, we have a rectangle that contains a square. In order to find the area of the shaded region, we simply do the following.
| Step 1 | Shaded region = area of the rectangle - area of the square |
| Step 2 | Area of the rectangle = 10*5 = 50 |
| Step 3 | Area of the square = 1*1 = 1 |
| Step 4 | Shaded region = 50-1 = 49 |
Solution Problem 3
Here, we know because of the notation that the sides marked with a dash are equal to each other. To find the shaded region, we simply need to find the area of the following triangle.
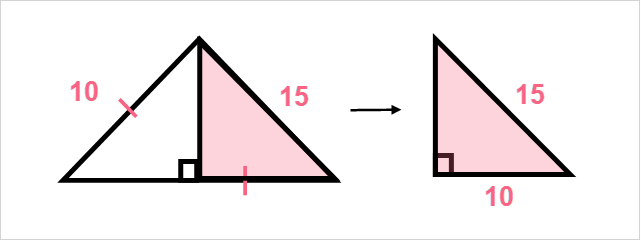
| Step 1 | Use Pythagorean theorem to find the height of the triangle: 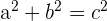 |
| Step 2 | 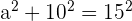
|
| Step 3 | 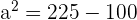 |
| Step 4 |  |
| Step 5 |  |













I’m just curious if the area between the polygon and the circumscribed circle has a name.
https://www.superprof.co.uk/resources/academic/maths/geometry/plane/orthocenter-centroid-circumcenter-and-incenter-of-a-triangle.html