Chapters

Axis Quadrants
| Axis | Points |
| X-axis | x |
| Y-axis | y |
As you can see, these axes split the plane into 4 quadrants. The quadrants run counter-clockwise and have special properties with regards to their coordinates.
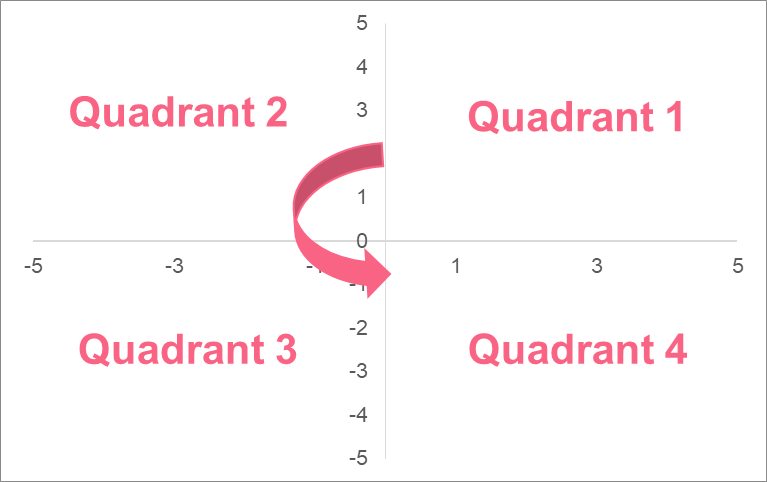
| Quadrant | Coordinates |
| I | (positive, positive) |
| II | (negative, positive) |
| III | (negative, negative) |
| IV | (positive, negative) |
Distance Between Points
When you’re measuring the distance between two points on a graph, the easiest way is to simply count the spaces between them.
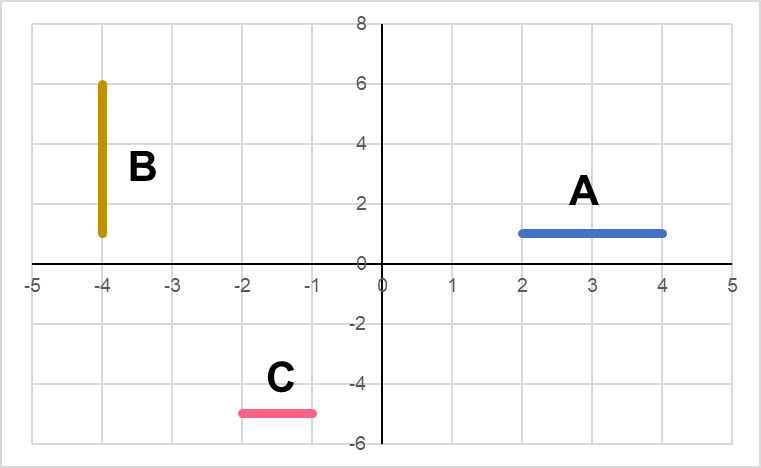
| A | 2 |
| B | 5 |
| C | 1 |
Easy enough. However, what would happen if you had the following points?
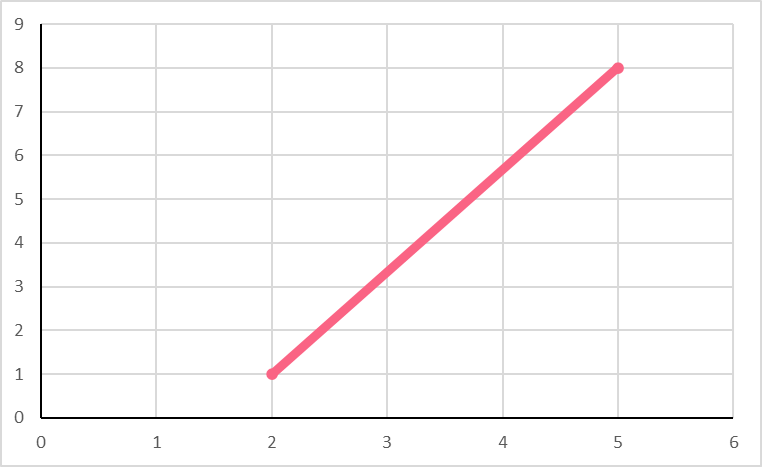
To find the distance between these two points, you can use the following formula.
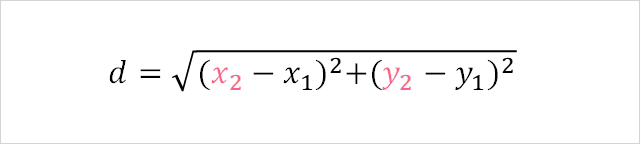
| Coordinates | |
| Point A | (x1,y1) |
| Point B | (x2,y2) |
Example 1
Let’s take the example from before and apply it now that we know the formula.
| Formula Coordinates | Coordinates | |
| Point A | (x1,y1) | (2,5) |
| Point B | (x2,y2) | (9,9) |
The first step is to replace the actual coordinates into the formula.

The next step is to solve for the distance by simplifying.

What is a Line?
A line is simply a set of points. That’s it! With one simple concept, we’re able to build up some pretty complex ideas. Let’s take a look at a couple of special lines.

| A | Line | A set of points |
| B | Parallel lines | Lines that never touch |
| C | Perpendicular lines | Lines that cross at a 90 degree angle |
A triangle can be thought of as a set of three points or even as a special set of lines. In fact, a right triangle contains two perpendicular lines. Take a look.

| A | Triangle | A set of 3 points or 3 lines |
| B | Right triangle | A set of 3 points or a set of 3 lines where 2 are perpendicular |
Distance of a Line Formula
The distance of a line can be summed up in one term: Pythagorean theorem. When dealing with right triangles, you can easily find the length of a line.

Take a look at some of the properties of these sides.
| a | b | c |
| Smaller side | Smaller side | Largest side |
As you can see, we always know that c is the largest side. This is because one of the properties of right triangles is that the side opposite of the right angle is always the largest.
Example 2
Let’s take the following as an example. You have a square and know that its diagonal has a length of 100.
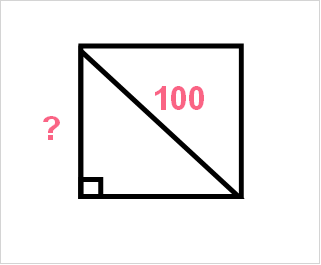
Do you know the length of the sides of the square? We can solve this by taking the following into account.
| Property 1 | A square is made up of four right triangles |
| Property 2 | The sides of a square are all the same length |
Because of this, we get the following triangle.
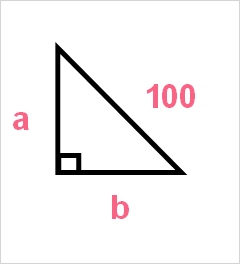
Recall that sides of squares are all the same length, which is what makes them a square. This means that a = b. This means that the formula becomes the following.
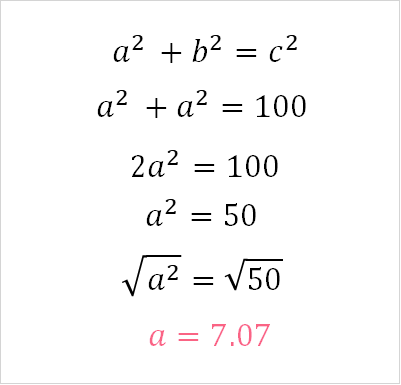
Distance to the Origin
When we want to know the distance of any point to the origin, we can use the distance of two points formula. Recall that the origin is the point in each graph where the axes meet. In other words, it is (0,0).
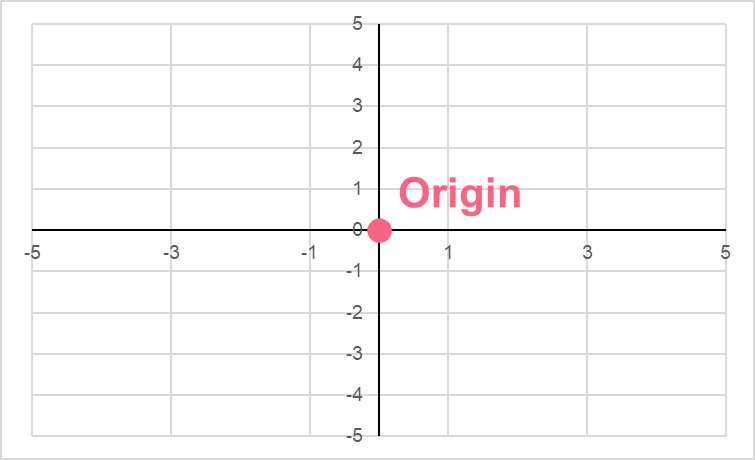
When we look at the distance of two points formula, we can see that we can replace one of the points by the origin.

This means that the formula for the distance becomes the following.
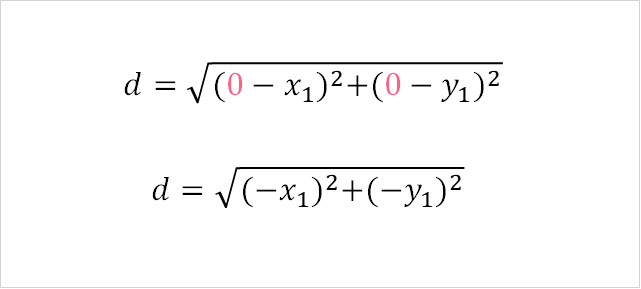
Example 3
Say that the centre of town is located at the origin. There is a new park that has been built at the point that is 30 meters to the left and 20 meters down from the park. Take a look:
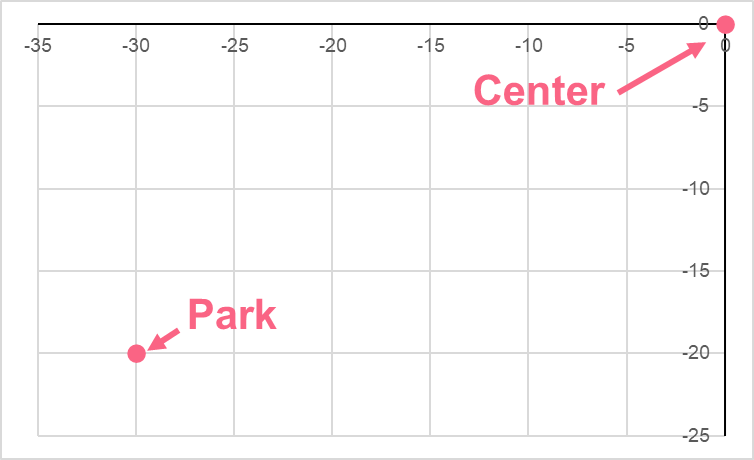
The city wants to build a road that goes from the centre of the town straight to the park. What is the shortest length of this street that they can build? To solve this, we simply need to use the modified distance formula.
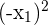 | 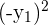 | d |
 | 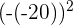 | 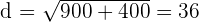 |
Distance Between Point and Line Using Distance
When we want to find the distance between any point and a line, we can simply take any point on that line and use the distance formula. Say that we have the following.
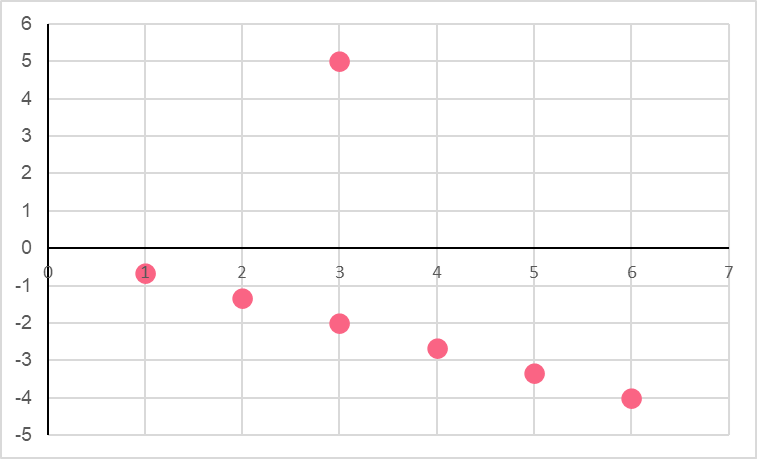
| Line Equation | y = (-2/3)x |
| Point | (3,5) |
We can simply plug in any x value to get the y value and plug these points into the distance formula. However, what if we want to find the shortest distance to the line? The shortest line will be perpendicular to the line.

Since perpendicular lines form a right angle, we simply have a right angle. Perpendicular lines have slopes that are reciprocals. So, the line that is formed by our point has the following slope.
| Slope of Line | Slope of Perpendicular |
| (-2/3) |  |
In order to find the y-intercept of the line, we simply plug in the point into the slope-intercept formula.
| Slope-Intercept | Perpendicular Line | Points | Solve for b | Formula |
| y=mx+b | y=(3/-2)x+b | 5=(3/-2)(3)+b | 5=b-4.5 b=9.5 | y=(3/-2)x+9.5 |
In order to find the point of intersection, or where the two lines meet, we simply have to set them equal to each other. This is because at that point, both lines take the same value.
| Equal | Solve for x | Plug in to find y |
| (-2/3)x = (3/-2)x+9.5 | x=11.4 | y = (-2/3)(11.4) = -7.6 |
Now, you have the point of intersection, all that’s left to do is find the distance between the point and the point of intersection.













