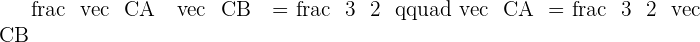As the word tells you, the midpoint formula finds the midpoint of a line segment. It doesn't matter how long the line is or in which direction it is, you can use this formula on any straight line you want. The only condition is that it should be a linear line, you can't use this formula on a curve. The generic definition is that a midpoint is a point on a line segment that divides the segment into two equal portions. Sometimes, it can become the point of symmetry but that is another discussion and we will discuss it later in this blog.
There are many formulas in coordinate geometry but there is something unique about the midpoint formula. This is the only formula in coordinate geometry that can find two coordinates in a single solution. Below is the formula to calculate the midpoint of a line segment:
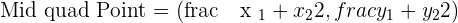
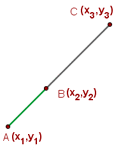
Imagine a line that starts from point A and ends to point B. To calculate the midpoint of this line, you need to have both points' coordinates.

The midpoint of this line is represented as M in the above picture. Since you have both points' coordinates, you can now use the midpoint formula to find the coordinates of M. Either you can use the above formula directly to find the midpoint or you can break it into two steps. Both methods are easy but the second method is a bit long but there is less probability of error. The first step is to add both points' x coordinate and then do the same with the y coordinate.
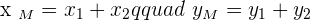
The second step is to divide both of them by  and that is how you find the midpoint using the second method:
and that is how you find the midpoint using the second method:
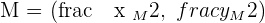

Examples
Calculate the coordinates of the midpoint from the line segment AB.

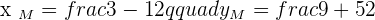
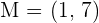
Calculate the coordinates of Point C in the line segment AC, knowing that the midpoint is  and an endpoint is
and an endpoint is 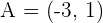 .
.

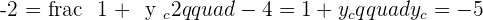

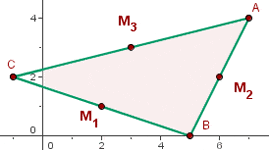
If 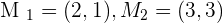 and
and 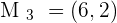 are the midpoints of the sides that make up a triangle, what are the coordinates of the vertices?
are the midpoints of the sides that make up a triangle, what are the coordinates of the vertices?
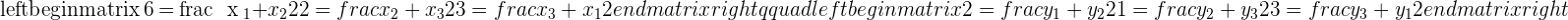
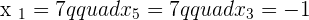


If the line segment AB with endpoints 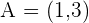 and
and 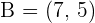 is divided into four equal parts, what are the coordinates of the points of division?
is divided into four equal parts, what are the coordinates of the points of division?

Q is the midpoint of AB
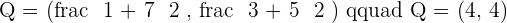
P is the midpoint of AQ

R is the midpoint of QB

Symmetric Point

Suppose a point A and another point A'. There is a midpoint between both points. If both points are equidistant from the midpoint and both points also match each other if one of them is rotated  then it is safe to say that the midpoint is the symmetry point. In simple words, if A' is symmetric of A with respect to M, then M is the midpoint of the line segment AA'.
then it is safe to say that the midpoint is the symmetry point. In simple words, if A' is symmetric of A with respect to M, then M is the midpoint of the line segment AA'.
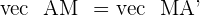
Calculate the symmetric point of 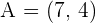 with the midpoint
with the midpoint  .
.

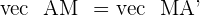
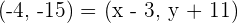
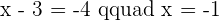
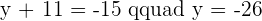
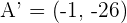
Calculate the symmetric point of 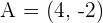 for midpoint
for midpoint 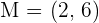 .
.
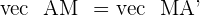


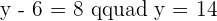

Three Collinear Points
The word collinear means that two or more objects or things lie on the same line. In the world of coordinate geometry, collinear points mean that two or more points that lie on the same line, no matter how far they are, will be collinear points.
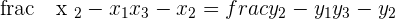
Determine whether  and
and 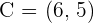 are alligned points.
are alligned points.
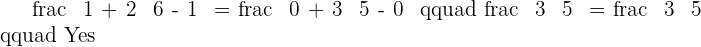
Calculate the value of a in the following aligned points.
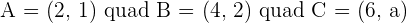
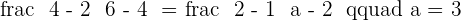
Centroid Coordinates

Every object in this universe has a centre point. In the physics domain, it is a very important thing. In fact, they have a separate sub-domain for it. Finding the centre isn't easy, there are different methods for finding a centre for different objects. In the case of triangles, we use the concept of the centroid. In coordinate geometry, centroid coordinates determine the centre of the triangle. It is found by three linear lines intersecting the centre of each side of the triangle. The point at which all three lines intersects is the point of centre, consider the above diagram as an example. Each side has a line that is passing through each side's centre respectively. Point G is the point where all three lines meet each other and it is the centre of the triangle. Below is the formula to find the centre coordinates of the triangle.
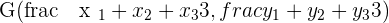
Please do note that this formula is only valid for a triangle, if you try to use this formula for other shapes or objects, it won't work.
Given the vertices of a triangle 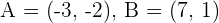 and
and 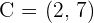 , calculate the coordinates of the centroid.
, calculate the coordinates of the centroid.


If two vertices of a triangle are 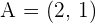 and
and  and the centroid is
and the centroid is 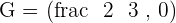 , calculate the third vertex.
, calculate the third vertex.
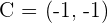
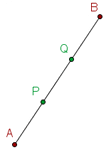
If you can find the midpoint of a segment, you can divide it into two equal parts. Finding the middle of each of the two equal parts allows you to find the points needed to divide the entire segment into four equal parts. Finding the middle of each of these segments gives you eight equal parts, and so on.
Dividing a Segment
You can divide a line segment into many equal parts. It depends on how many parts you want but one thing is for sure that all those parts will be equal. Divide a line segment into two parts by finding its midpoint. Now you have two parts, starting of the line till the midpoint and from the midpoint to the endpoint. Now find the midpoints of both sections. Now you have four different parts. Keep doing this for dividing the segment into more parts. Dividing the segment AB at a given ratio r is to determine a point P on the line containing the segment AB so that both sides PA and PB have a ratio of:

Calculate the points P and Q that divide the line segment with endpoints  and
and  into three equal parts?
into three equal parts?
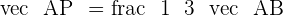
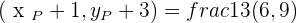
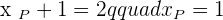
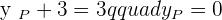
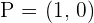

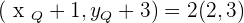

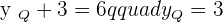
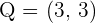
The coordinates of the endpoints from the line segment AB are:  and
and 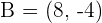 . Find the coordinates of point C such that it divides the line segment into two equal parts.
. Find the coordinates of point C such that it divides the line segment into two equal parts.




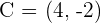
Given the points,  and
and 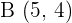 , find a point C such that it is aligned with A and B, and a ratio of
, find a point C such that it is aligned with A and B, and a ratio of  is obtained.
is obtained.